练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（　　）

    A. 2对 B. 3对 C. 4对 D. 5对

    【答案】C

    【解析】试题分析：∵四边形ABCD是正方形，∴AB=CD=CB=AD，∠A=∠C=∠ABC=∠ADC=90°，AD∥BC，在△ABD和△BCD中，∵AB=BC，∠A=∠C，AD=CD，∴△ABD≌△BCD，∵AD∥BC，∴∠MDO=∠M′BO，在△MOD和△M′OB中，∵∠MDO=∠M'BO，∠MOD=∠M'OB，DM=BM'，∴△MDO≌△M′BO，同理可证△NOD≌△N′OB，∴△MON≌△M′ON′，∴全等三角形一共有4对．故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有一个老太太提着一个篮子去卖鸡蛋，第一个人买走了她的鸡蛋的一半又半个；第二个人买走了剩下的一半又半个；第三人买走了前两个人剩下的一半又半个，正好卖完全部鸡蛋，问老太太一共卖了多少个鸡蛋．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面内直角坐标系中，直线l：y= x+1交x轴于点A，交y轴于点B，点A1 ， A2 ， A3 ， …在x轴上，点B1、B2、B3 ， …在直线l上．若△OB1A1 ， △A1B2A2 ， △A2B3A3 ， …均为等边三角形，则OAn的长是（ ）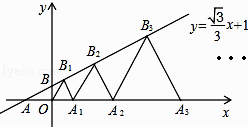

    A.2n
    B.（2n+1）
    C.（2n﹣1﹣1）
    D.（2n﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线L：y=ax2+bx+c与已知抛物线y= x2的图像的形状相同，开口方向也相同，且顶点坐标为（﹣2，﹣4）
    （1）求L的解析式；
    （2）若L与x轴的交点为A，B（A在B的左侧），与y轴的交点为C，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列等式的规律，解答下列问题：

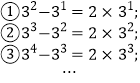
    （1）按此规律，第④个等式为_________；第个等式为_______；（用含的代数式表示，为正整数）

    （2）按此规律，计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（ ）
    A.a2+a3=a5
    B.（﹣2a2）3÷（ ）2=﹣16a4
    C.3a﹣1=
    D.（2 a2﹣ a）2÷3a2=4a2﹣4a+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

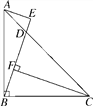
    【题目】如图，在Rt△ABC中，∠ABC＝90°，AB＝BC，D是AC上一点，AE⊥BD，交BD的延长线于E，CF⊥BD于F.

    (1)求证：CF＝BE；

    (2)若BD＝2AE，求证：∠EAD＝∠ABE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图①中△ABC是等边三角形，其边长是3，图②中△DEF是等腰直角三角形，∠F＝90°，DF＝EF＝3.

    (1)若S1为△ABC的面积，S2为△DEF的面积，S3＝AB·BC·sinB，S4＝DE·DF·sinD，请通过计算说明S1与S3，S2与S4之间有着怎样的关系；

    (2)在图③中，∠P＝α(α为锐角)，OP＝m，PQ＝n，△OPQ的面积为S，请你根据第(1)小题的解答，直接写出S与m，n以及α之间的关系式，并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1的7张长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）

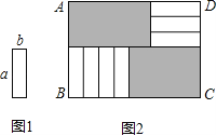
    A. a=b B. a=2b

    C. a=3b D. a=4b

    查看答案和解析>>

    同步练习册答案