
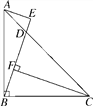
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
【答案】(1)见解析;(2)见解析.
【解析】(1)根据已知条件证明△ABE≌△BCF即可求证CF=BE.
(2)由(1)可知:∠ABE=∠BCF,且AE∥CF所以∠EAD=∠ACF,只需证明∠ABE=∠BCF=∠ACF即可证明出∠EAD=∠ABE.
证明:(1)∵∠ABC=90°,CF⊥BD,AE⊥BD,
∴∠ABE+∠EBC=90°=∠EBC+∠BCF,
∴∠ABE=∠BCF.
又∵∠AEB=∠BFC=90°,AB=CB,
∴△ABE≌△BCF,
∴CF=BE.
(2)由(1)知△ABE≌△BCF,
∴BF=AE,∠ABE=∠BCF.又∵BD=BF+FD=2AE,
∴BF=DF.
又∵CF⊥BD于F,∴CB=CD,
∴CF平分∠ACB.
又∵∠AEB=∠CFD=90°,
∴AE∥CF,∴∠EAD=∠ACF.
∵∠ABE=∠BCF=∠ACF,
∴∠EAD=∠ABE.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.
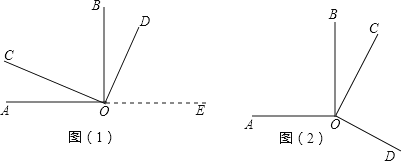
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB= ![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
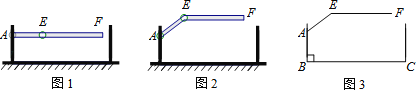
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E. 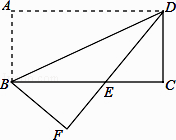
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(教材回顾)课本88页,有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)三角形有3个顶点,如果在它的内部再画n个点,并以这(n+3)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
三角形内点的个数 | 图形 | 最多剪出的小三角形个数 |
1 |
| 3 |
2 |
| 5 |
3 |
| 7 |
… | … | … |
(问题解决)
(1) 当三角形内有4个点时,最多剪得的三角形个数为______________;
(2) 你发现的变化规律是:三角形内的点每增加1个,最多剪得的三角形增加______个;
(3) 猜想:当三角形内点的个数为n时,最多可以剪得_______________个三角形;
像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
(4)请你尝试用归纳的方法探索1+3+5+7+…+(2n-1)+(2n+1)的和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海警船在A处发现北偏东30°方向相距12海里的B处有一艘可疑货船,该艘货船以每小时10海里的速度向正东航行,海警船立即以每小时14海里的速度追赶,到C处相遇,求海警船用多长时间追上了货船?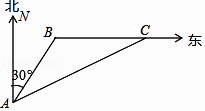
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com