
分析 (1)根据题意可知,一辆车发生故障时,没有发生故障的车与医生是同向行驶问题,到没有发生故障的车再返回接步行的医生是相向行驶问题,然后接到医生再返回县城是单向行驶问题,只要将这三段的时间计算出来求出它们的和与45分钟做比较即可解答本题;
(2)设计的方案只要符合要求即可,步行的医生休息一段时间的路程正好是汽车行驶的这段路程的2倍,然后求出这段时间即可解答命题.
解答 解:(1)按照这个方案行进,能保证整个医疗小组在规定时间前全部赶到芦山县城.
理由:由题意可得,
设没出故障的车从距芦山县城19.5千米到县城用的时间为t1小时,再次与步行医生相遇用的时间为t2小时,相遇后再返回县城用的时间为t3小时,
${t}_{1}=\frac{19.5}{60}=\frac{13}{40}$,
${t}_{2}=\frac{19.5-5×\frac{13}{40}}{60+5}$=$\frac{143}{520}$,
${t}_{3}=\frac{19.5-5×\frac{13}{40}-5×\frac{143}{520}}{60}$=$\frac{143}{520}$,
${t}_{1}+{t}_{2}+{t}_{3}=\frac{13}{40}+\frac{143}{520}+\frac{143}{520}=\frac{91}{104}$小时=52.5分,
∵52.5<54,
∴按照这个方案行进,能保证整个医疗小组在规定时间前全部赶到芦山县城;
(2)方案是:搭乘发生故障小车的4个人下车步行,中间休息2分钟,另一辆车将车内4人送到芦山县城后,立即返回接步行的4个人到芦山县城.
没出故障的车从距芦山县城19.5千米到最后全部医生到达县城用的时间为:52.5+$\frac{\frac{2}{60}×5×2}{60}×60=52.5+\frac{1}{3}$=52.888<54,
故此方案可行.
点评 本题考查一元一次方程的应用,解题的关键是明确题意,列出相应的方程,找出所求问题需要的条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,一次函数的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(m,6)和点B(4,-3).
如图,一次函数的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(m,6)和点B(4,-3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
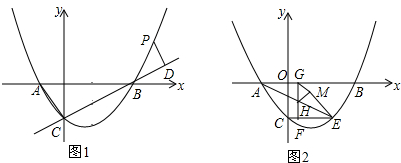
 如图,抛物线y=$\frac{1}{2}$x2+bx+c与直线l:y=kx+m交于A(4,2)、B(0,-1)两点.
如图,抛物线y=$\frac{1}{2}$x2+bx+c与直线l:y=kx+m交于A(4,2)、B(0,-1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
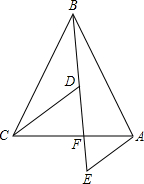 如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com