
【题目】如图,在□ABCD中,对角线AC , BD相交于点O , E , F是对角线AC上的两点,当点E , F满足下列哪个条件时,四边形DEBF不一定是平行四边形( ) 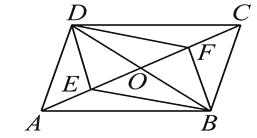
A.AE=CF
B.∠AED=∠CFB
C.∠ADE=∠CBF
D. DE=BF
【答案】D
【解析】A,∵AE=CF ,
∴OE=OF ,
∵DO=BO ,
∴四边形DEBF是平行四边形.
B,∵∠AED=∠CFB ,
∴∠DEO=∠BFO ,
∴△DOE ≌△BOF ,
∴EO=FO ,
∴四边形DEBF是平行四边形.
同理若∠ADE=∠CBF , 也能证明△DOE ≌△BOF , 从而四边形DEBF是平行四边形.只有答案D不能证明.
故选D.
【考点精析】根据题目的已知条件,利用平行四边形的判定的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】南京地铁4号线将于年内开工,全长约33200m,将33200用科学记数法表示应为( )
A.3.32×104B.33.2×103C.332×102D.0.332×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知n正整数,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.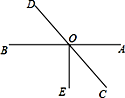
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.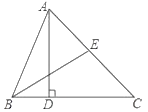
(1)求∠CAD和∠BAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,试求∠BEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏季来临,商场准备购进甲、乙两种空调.已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同.请解答下列问题:(1)求甲、乙两种空调每台的进价;
(2)若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润y(元)与甲种空调x(台)之间的函数关系式;
(3)在(2)的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器.直接写出购买按摩器的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们的生活中处处都能体现出数学知识的应用,当我们在植树的时候,要整齐地栽一行树,只要确定两端树坑的位置就可以了.这一方法用数学知识解释其道理为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A.B两种型号车的进货和销售价格如表:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com