
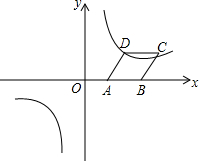
 平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.
平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.分析 (1)过点C作CE⊥AB于点E,设菱形的边长为x,则BC=AB=x,BE=10-2-x,在Rt△BEC中,利用勾股定理建立关于x的方程,解方程求出x的值即可;
(2)设双曲线的解析式为y=$\frac{k}{x}$,过点D作DF⊥AB于点F,分别求出OF,DF的长,则点D的坐标可知,代入双曲线的解析式求出k的值即可.
解答 解:(1)设菱形的边长为x,则BC=AB=x,BE=10-2-x,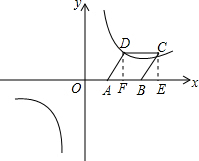
∵点C(10,4),
∴CE=4,
在Rt△BEC中,由勾股定理可得:BC2=BE2+CE2,
即x2=(10-2-x)2+42,
解得:x=5,
∴菱形ABCD的边长为5;
(2)设双曲线的解析式为y=$\frac{k}{x}$,过点D作DF⊥AB于点F,
∵DC∥AB,点C(10,4),
∴DF=4,
∵AB=5,
∴OF=OE-EF=10-5=5,
∴点D(5,4),
∴k=20,
∴$y=\frac{20}{x}$.
点评 本题考查了菱形的性质、勾股定理的运用、解一元二次方程以及利用待定系数法求双曲线的解析式,解题的关键是做高线,构造直角三角形,利用勾股定理求出菱形的边长.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:选择题
| A. | (2,-3) | B. | (-2,-3) | C. | (2,3) | D. | (-1,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).
如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,$2\sqrt{3}}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com