
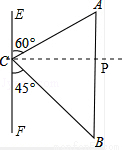
如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据: ≈1.41,
≈1.41, ≈2.45)
≈2.45)

小岛A与小岛B之间的距离是100km.
【解析】
试题分析:
先过点C作CP⊥AB于P,根据已知条件求出∠PCB=∠PBC=45°,∠CAP=60°,再根据轮船的速度和航行的时间求出BC的值,在Rt△PCB中,根据勾股定理求出BP=CP的值,再根据特殊角的三角函数值求出AP的值,最后根据AB=AP+PB,即可求出答案.
试题解析:
【解析】
过点C作CP⊥AB于P,
∵∠BCF=45°,∠ACE=60°,AB∥EF,
∴∠PCB=∠PBC=45°,∠CAP=60°,
∵轮船的速度是45km/h,轮船航行2小时,
∴BC=90,
∵BC2=BP2+CP2,
∴BP=CP=45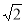 ,
,
∵∠CAP=60°,
∴tan60°=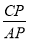 =
=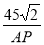 ,
,
∴AP=15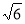 ,
,
∴AB=AP+PB=15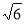 +45
+45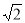 =15×2.45+45×1.41≈100(km).
=15×2.45+45×1.41≈100(km).
答:小岛A与小岛B之间的距离是100km.
考点:解直角三角形的应用-方向角问题


科目:初中数学 来源:2014年初中毕业升学考试(湖南株洲卷)数学(解析版) 题型:填空题
直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(﹣2,0),且两直线与y轴围城的三角形面积为4,那么b1﹣b2等于 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南岳阳卷)数学(解析版) 题型:解答题
如图,抛物线经过点A(1,0),B(5,0),C(0, )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
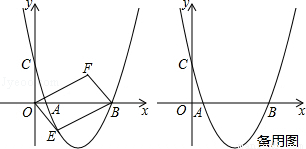
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南岳阳卷)数学(解析版) 题型:选择题
下列因式分解正确的是( )
A.x2﹣y2=(x﹣y)2 B.a2+a+1=(a+1)2
C.xy﹣x=x(y﹣1) D.2x+y=2(x+y)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:解答题
如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南娄底卷)数学(解析版) 题型:填空题
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为 m.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
三峡大坝全长约2309米,这个数据用科学记数法表示为( )米.

A. 2.309×103 B. 23.09×102 C. 0.2309×104 D. 2.309×10﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com