
已知二次函数y=﹣x2+bx+c的对称轴为x=2,且经过原点,直线AC解析式为y=kx+4,
(1)求二次函数解析式;
(2)若 =
= ,求k;
,求k;
(3)若以BC为直径的圆经过原点,求k.

(1)二次函数解析式:y=﹣x2+4x.
(2)k=﹣1.
(3)k=﹣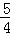 .
.
【解析】
试题分析:(1)根据对称轴为x=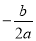 =2,且函数过(0,0),则可得出b,c,从而得到函数解析式.
=2,且函数过(0,0),则可得出b,c,从而得到函数解析式.
(2)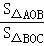 =
= ,而且这两个三角形为同高不同底的三角形,易得
,而且这两个三角形为同高不同底的三角形,易得 =
= ,考虑计算方便可作B,C对x轴的垂线,进而有B,C横坐标的比为
,考虑计算方便可作B,C对x轴的垂线,进而有B,C横坐标的比为 =
=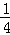 .由B,C为直线与二次函数的交点,则联立可求得B,C坐标.由上述倍数关系,则k易得.
.由B,C为直线与二次函数的交点,则联立可求得B,C坐标.由上述倍数关系,则k易得.
(3)以BC为直径的圆经过原点,易得∠BOC=90°,由(2)可发现B,C横纵坐标恰好可表示出EB,EO,OF,OC.而由∠BOC=90°,易证△EBO∽△FOC,即EB•FC=EO•FO.由此构造方程即可得k值.
试题解析:(1)∵二次函数y=﹣x2+bx+c的对称轴为x=2,且经过原点,
∴﹣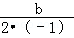 =2,0=0+0+c,
=2,0=0+0+c,
∴b=4,c=0,
∴y=﹣x2+4x.
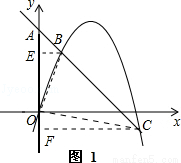
(2)如图1,连接OB,OC,过点B作BE⊥y轴于E,过点C作CF⊥y轴于F,
∵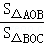 =
=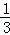 ,
,
∴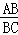 =
=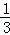 ,
,
∴ =
=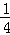 ,
,
∵EB//FC,
∴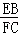 =
=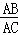 =
=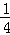 .
.
∵y=kx+4交y=﹣x2+4x于B,C,
∴kx+4=﹣x2+4x,即x2+(k﹣4)x+4=0,
∴△=(k﹣4)2﹣4•4=k2﹣8k,
∴x=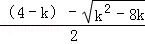 ,或x=
,或x=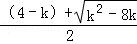 ,
,
∵xB<xC,
∴EB=xB=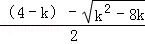 ,FC=xC=
,FC=xC=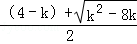 ,
,
∴4•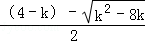 =
=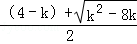 ,
,
解得 k=9(交点不在y轴右边,不符题意,舍去)或k=﹣1.
∴k=﹣1.
(3)∵∠BOC=90°,
∴∠EOB+∠FOC=90°,
∵∠EOB+∠EBO=90°,
∴∠EBO=∠FOC,
∵∠BEO=∠OFC=90°,
∴△EBO∽△FOC,
∴ ,
,
∴EB•FC=EO•FO.
∵xB=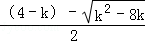 ,xC=
,xC=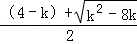 ,且B、C过y=kx+4,
,且B、C过y=kx+4,
∴yB=k•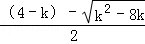 +4,yC=k•
+4,yC=k•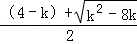 +4,
+4,
∴EO=yB=k•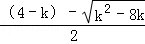 +4,OF=﹣yC=﹣k•
+4,OF=﹣yC=﹣k•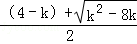 ﹣4,
﹣4,
∴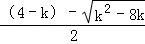 •
•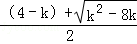 =(k•
=(k•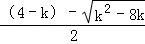 +4)•(﹣k•
+4)•(﹣k•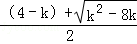 ﹣4),
﹣4),
整理得 16k=﹣20,
∴k=﹣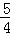 .
.
考点:1、函数图象交点的性质;2、相似三角形性质;3、一元二次方程;4、圆周角定理


科目:初中数学 来源:2014年初中毕业升学考试(湖南郴州卷)数学(解析版) 题型:填空题
如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:选择题
下列命题是真命题的是( )
A.四条边都相等的四边形是矩形
B.菱形的对角线相等
C.对角线互相垂直的平行四边形是正方形
D.对角线相等的梯形是等腰梯形
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:选择题
小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )

A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C.小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
| A型 | B型 |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:解答题
某校枇杷基地的枇杷成熟了,准备请专业摘果队帮忙摘果,现有甲、乙两支专业摘果队,若由甲队单独摘果,预计6天才能完成,为了减少枇杷因气候变化等原因带来的损失,现决定由甲、乙两队同时摘果,则2天可以完成,请问:
(1)若单独由乙队摘果,需要几天才能完成?
(2)若有三种摘果方案,方案1:单独请甲队;方案2:同时请甲、乙两队;方案3:单独请乙队.甲队每摘果一天,需支付给甲队1000元工资,乙队每摘果一天,须支付给乙队1600元工资,你认为用哪种方案完成所有摘果任务需支付给摘果队的总工资最低?最低总工资是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com