
| 3 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
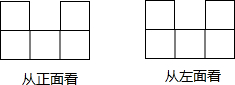 如图所示的几何体是由若干块小正方体堆积而成从正面看和从左面所看到的图形.请结合这两幅图,写出这个几何体最少要多少块小立方体组成?并画出你从上面看到的图形的所有可能(注:在小立方块上标数字,以表示该处小立方块的块数).
如图所示的几何体是由若干块小正方体堆积而成从正面看和从左面所看到的图形.请结合这两幅图,写出这个几何体最少要多少块小立方体组成?并画出你从上面看到的图形的所有可能(注:在小立方块上标数字,以表示该处小立方块的块数).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com