
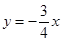 ;(3)P点的坐标为标为
;(3)P点的坐标为标为 、
、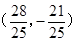 、
、 、
、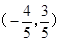 .
.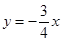 ;(3)由点P在直线OD上,可设P点的坐标为
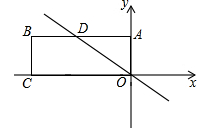
;(3)由点P在直线OD上,可设P点的坐标为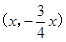 ,当以P、A、D三点为顶点的三角形是等腰三角形时,应分三种情况讨论:即①PA=PD;②AP=AD;③DP=DA;分别就三种情况求出P点的坐标.
,当以P、A、D三点为顶点的三角形是等腰三角形时,应分三种情况讨论:即①PA=PD;②AP=AD;③DP=DA;分别就三种情况求出P点的坐标.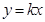 ,
,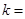
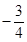
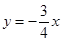
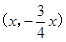 ,当以P、A、D三点为顶点的三角形是等腰三角形时,分三种情况:
,当以P、A、D三点为顶点的三角形是等腰三角形时,分三种情况: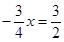
 .
.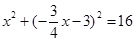
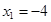 (与D点重合舍去),
(与D点重合舍去),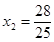
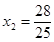 时,
时,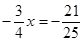
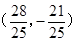
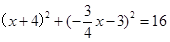
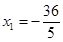 ,
,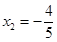
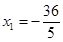 时,
时,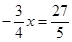 ;
;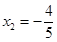 时,
时,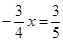 .
. ,
,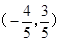 .
. 、
、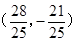 、
、 、
、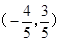 .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, ),
),
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
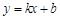 与反比例函数
与反比例函数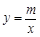 的图象交于A(2,1),B(-1,
的图象交于A(2,1),B(-1,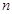 )两点.
)两点.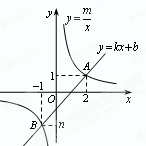
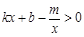 的解集.
的解集.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ,求线段AE所在直线的解析式.
,求线段AE所在直线的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com