练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    计算
    （1）3x2•（-x）2÷x   
    （2）（x+2）（x-3）
    （3）（3a+b）2
    （4）（a+1）（a-1）-（a+1）2．
    考点：整式的混合运算
    专题：
    分析：（1）先算乘方，再算乘除；
    （2）先算乘法，再合并同类项即可；
    （3）根据完全平方公式进行计算即可；
    （4）先算乘法，再合并同类项即可．
    解答：解：（1）原式=3x2•x2÷x
    =3x3；

    （2）原式=x2-3x+2x-6
    =x2-x-6；

    （3）原式=9a2+6ab+b2；

    （4）原式=a2-1-a2-2a-1
    =-2a-2．
    点评：本题考查了整式的混合运算的应用，主要考查学生的计算能力，题目比较好，难度适中．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知24-n•42n+1=8-n，则n的值为（　　）
    A、n=-3B、n=-2
    C、n=-1D、n=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

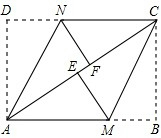    已知：如图，在矩形ABCD中，把∠B、∠D分别翻折，使点B、D分别落在对角线BC上的点E、F处，折痕分别为CM、AN．
    （1）求证：△ADN≌△CBM．
    （2）请连接MF、NE，证明四边形MFNE是平行四边形，四边形MFNE是菱形吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，四边形ABCD、BEFG均为正方形．

    （1）如图1，连接AG、CE，试判断AG和CE的数量关系和位置关系并证明．
    （2）将正方形BEFG绕点B顺时针旋转β角（0°＜β＜180°），如图2，连接AG、CE相交于点M，连接MB，当角β发生变化时，∠EMA的度数是否发生变化？若不变化，求出∠EMA的度数；若发生变化，请说明理由．
    （3）在（2）的条件下，∠EMB的度数是否是定值？若是，求出∠EMB的度数；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

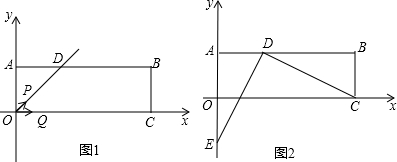
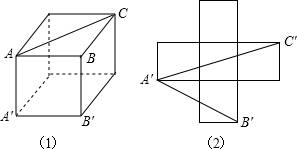    图（1）为一个无盖的正方体纸盒，现将其展开成平面图，如图（2）．已知展开图中每个正方形的边长为1．
    （1）求该展开图中可画出最长线段的长度，并求出这样的线段可画几条．
    （2）试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

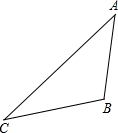    如图，游客从某旅游区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C；另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为45m/min．在甲出发2min后，乙开始从A乘缆车到B，在B处停留5min后，再从B匀速步行到C，二人同时到达．已知缆车匀速直线运动的速度为180m/min，山路AC长为2430m，且测得∠CBA=45°，∠CBA=105°．（参考数据：
    		2
    ≈1.4，
    		3
    ≈1.7）．
    （1）求索道AB的长；
    （2）求乙的步行速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：（1-3y）2+2（3y-1）=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系xOy中，矩形OABC过原点O，且A（0，2）、C（6，0），∠AOC的平分线交AB于点D．
    （1）直接写出点B的坐标；
    （2）如图1，点P从点O出发，以每秒
    		2
    个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒．
    ①当t为何值时，△OPQ的面积等于1；
    ②当t为何值时，△PQB为直角三角形；
    （3）如图2，点E（0，-2），连接DC、DE，将∠CDE绕点D顺时针旋转，两边DC、DE与x轴、y轴分别交于点M、N，若△DEN为等腰三角形，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）（
    2
    3
    ）5×35
    （2）315÷313．

    查看答案和解析>>

    同步练习册答案