
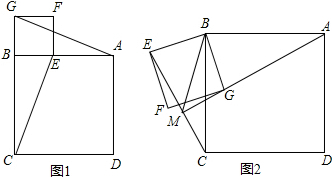
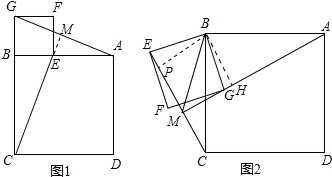
 解:(1)AG=EC,AG⊥EC,理由为:
解:(1)AG=EC,AG⊥EC,理由为:
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| A、不赔不赚 | B、赔100元 |
| C、赚100元 | D、赚360元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 物流公司在收取了一客户的450元运费后,需要将货物从A点发出,分别运到B,C,D三处,然后再返回A点,所走的路程如图所示,若四边形ABCD可以看作是平行四边形,当司机从A跑到B发现里程表跑了30千米,从B跑到C发现比A到B多跑了40千米,若该汽车每100千米耗油13升,每升汽油7.35元,车辆磨损和司机工资200元,那么该公司是盈利还是亏损?
物流公司在收取了一客户的450元运费后,需要将货物从A点发出,分别运到B,C,D三处,然后再返回A点,所走的路程如图所示,若四边形ABCD可以看作是平行四边形,当司机从A跑到B发现里程表跑了30千米,从B跑到C发现比A到B多跑了40千米,若该汽车每100千米耗油13升,每升汽油7.35元,车辆磨损和司机工资200元,那么该公司是盈利还是亏损?查看答案和解析>>
科目:初中数学 来源: 题型:
| AE |
| BE |
| DF |
| CF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com