练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△OAB是边长为2＋的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在边OB上，记为，折痕为EF．

    (1)当E∥x轴时，求点和E的坐标；

    (2)当E∥x轴，且抛物线y＝－x2＋bx＋c经过点和E时，求该抛物线与x轴的交点的坐标；

    (3)当点在OB上运动但不与点O、B重合时，能否使△EF成为直角三角形？若能，请求出此时点的坐标；若不能，请你说明理由．

    答案：
    解析：

    　　(1)当平行于x轴时，∠=．因为△ABO为等边三角形，所以∠OE=，∠EO=，O=ED．设O=a，则OE=2a．

    　　在Rt△OE中，tan∠OE=，即=，所以E=a=AE．

    　　∵AE+OE=2+，2a+=2+，∴a=O=1，E=．

    　　∴(0，1)，E(，1)

    　　(2)由题设点(0，1)，E(，1)在y=x2+bx+c的图象上，则得方程组

    　　解得∴y=－＋1．当y=0时．得－x2＋x＋1=0．

    　　解得x1=，x2=

    　　∴抛物线与x轴的交点坐标为(2,0)，(－，0)

    　　(3)不能．因为要使△EF为直角三角形，则角只能是∠EF或∠FE．若∠EF=，因为△FE与△FAE关于FE对称，所以∠EF=∠AEF=，∠AE－．此时A、E、应在同一直线上，点应与O点重合，这与题设矛盾，所以∠EF≠，即△EF不能为直角三角形．同理．∠FE=也不成立，即△EF不能为直角三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

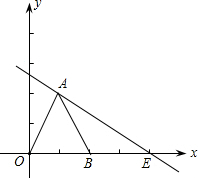    精英家教网如图，△OAB是边长为2的等边三角形，过点A的直线y=-
    		3 
    3
    x    +m与x轴交于点E．
    （1）求点E的坐标；
    （2）求过A、O、E三点的抛物线解析式；
    （3）若点P是（2）中求出的抛物线AE段上一动点（不与A、E重合），设四边形OAPE的面积为S，求S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△OAB是边长为4+2
    		3
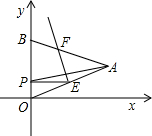    的等边三角形，其中O是坐标原点，顶点B在y轴的正半轴上．将△精英家教网OAB折叠，使点A与OB边上的点P重合，折痕与OA、AB的交点分别是E、F．如果PE∥x轴，
    （1）求点P、E的坐标；
    （2）如果抛物线y=-
    1
    2
    x2+bx+c经过点P、E，求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△OAB是边长为2+
    		3
    的等边三角形，其中O是坐标原点，顶点B在y轴正方向上，将△OAB折叠，使点A落在边OB上，记为A′，折痕为EF．
    （1）当A′E∥x轴时，求点A′和E的坐标；
    （2）当A′E∥x轴，且抛物线y=-
    1
    6
    x2+bx+c经过点A′和E时，求抛物线与x轴的交点的坐标；
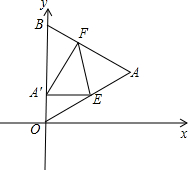    （3）当点A′在OB上运动，但不与点O、B重合时，能否使△A′EF成为直角三角形？精英家教网若能，请求出此时点A′的坐标；若不能，请你说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△OAB是边长为2+
    		3
    的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在OB边上，记为A′，折痕为EF．
    （1）当A′E∥x轴时，求点A'的坐标和直线A′F所对应的函数关系式；
    （2）在OB上是否存在点A′，使四边形AFA′E是菱形？若存在，请求出此时点A′的坐标；若不存在，请说明理由；
    （3）当点A′在OB上运动但不与点O、B重合，能否使△A′EF成为直角三角形？若能，请求出此时点A′的坐标；若不能，请你说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△OAB是边长为2+
    		3
    的等边三角形，其中O是坐标原点，顶点B在y轴正方向上，将△OAB 折叠，使点A落在边OB上，记为A′，折痕为EF．
    （1）当A′E∥x轴时，求点A′和E的坐标；
    （2）当A′E∥x轴，且抛物线y=-
    1
    6
    x2+bx+c    经过点A′和E时，求抛物线与x轴的交点的坐标．

    查看答案和解析>>

    同步练习册答案