
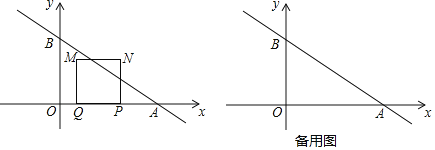
【题目】如图,在平面直角坐标系中,一次函数y=-![]() x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)当正方形PQMN的边MN经过点B时,t= 秒;
(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)连结BN,则BN的最小值为 .
【答案】(1)![]() ;(2)①当0<t≤1时,S=
;(2)①当0<t≤1时,S=![]() t2;②当1<t≤
t2;②当1<t≤![]() 时,∴S=﹣
时,∴S=﹣![]() t2+18t;③当
t2+18t;③当![]() <t≤2时, S=﹣3t2+12;(3)
<t≤2时, S=﹣3t2+12;(3)![]() .
.
【解析】
(1) 根据y=-![]() x+4容易得出A(6,0),B(0,4),所以当正方形PQMN的边MN经过点B时,正方形边长为4,则PQ=AP=4,进一步求出t=
x+4容易得出A(6,0),B(0,4),所以当正方形PQMN的边MN经过点B时,正方形边长为4,则PQ=AP=4,进一步求出t=![]() ;
;
(2)分三种情况,①利用正方形的面积减去三角形的面积,②利用矩形的面积减去三角形的面积,③利用梯形的面积,即可得出结论;
(3)先找出点N的运动轨迹所在直线的解析式,再用面积求高的方法求出BN的最小值.
解:(1)分别令x=0,y=0,可得 A(6,0),B(0,4),故OB=4.
∴当正方形PQMN的边MN经过点B时,正方形边长为4,则PQ=AP=4,
∴t=![]() ;
;
(2)(2)当点Q在原点O时,OA=6,
∴AP=![]() OA=3,
OA=3,
∴t=3÷3=1,
①当0<t≤1时,如图1,
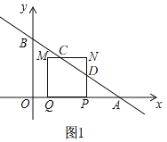
令x=0,
∴y=4,
∴B(0,4),
∴OB=4,
∵A(6,0),
∴OA=6,
在Rt△AOB中,tan∠OAB=![]() =
=![]() ,
,
由运动知,AP=3t,
∴P(6-3t,0),
∴Q(6-6t,0),
∴PQ=AP=3t,
∵四边形PQMN是正方形,
∴MN∥OA,PN=PQ=3t,
在Rt△APD中,tan∠OAB=![]() =
=![]() =
=![]() ,
,
∴PD=2t,
∴DN=t,
∵MN∥OA
∴∠DCN=∠OAB,
∴tan∠DCN=![]() =
=![]() =
=![]() ,
,
∴CN=![]() t,
t,
∴S=S正方形PQMN-S△CDN=![]() -
-![]() t×
t×![]() t=
t=![]() t2;
t2;
②当1<t≤![]() 时,如图2,
时,如图2,
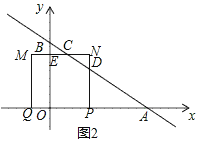
同①的方法得,DN=t,CN=![]() t,
t,
∴S=S矩形OENP-S△CDN=3t×(6-3t)-![]() t×
t×![]() t=-
t=-![]() t2+18t;
t2+18t;
③当![]() <t≤2时,如图3,S=S梯形OBDP=
<t≤2时,如图3,S=S梯形OBDP=![]() (2t+4)(6-3t)=-3t2+12;
(2t+4)(6-3t)=-3t2+12;
∴①当0<t≤1时,S=![]() t2;②当1<t≤
t2;②当1<t≤![]() 时,∴S=﹣
时,∴S=﹣![]() t2+18t;③当
t2+18t;③当![]() <t≤2时, S=﹣3t2+12;
<t≤2时, S=﹣3t2+12;
(3)如图,
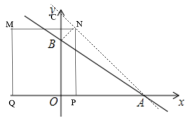
设点N的运动轨迹所在直线解析式为y=kx+b.由AP=PN=3t,可知当t=1时,N(3,3),且直线过A(6,0),易得解析式为y=-x+6.当x=0时,y=6.
直线y=-x+6与y轴交于点C,则C(0,6).可得OC=6,BC=6-4=2.AC=6![]()
∴S△ABC=![]() ×6×2=6,
×6×2=6,
当BN⊥AC时,BN最小.
S△ABC=![]() BN×AC,
BN×AC,
∴BN=![]() =
=![]()
故答案为![]()


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,顶点为
,顶点为![]() .
.

(1)求这条抛物线表达式;
(2)将该抛物线向右平移,平移后的新抛物线顶点为![]() ,它与
,它与![]() 轴交点为
轴交点为![]() ,联结
,联结![]() 、
、![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的正切值;
的正切值;
(3)联结![]() ,在(2)的条件下,射线
,在(2)的条件下,射线![]() 平分
平分![]() ,求点
,求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.
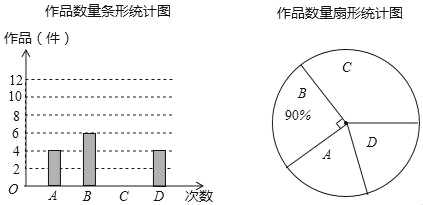
请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
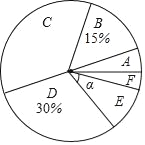
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分) 青少年沉迷于手机游戏,严重危害他们的身心健康,此问题已引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的“王者荣耀”玩家进行了简单的随机抽样调查,绘制出以下两幅统计图.
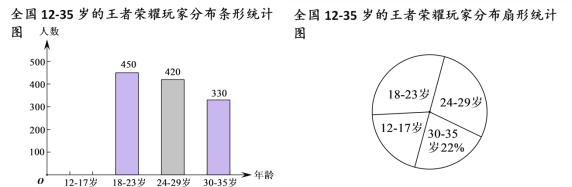
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是_________;
(3)据报道,目前我国12﹣35岁“王者荣耀”玩家的人数约为2000万,请估计其中12﹣23岁的人数.
(4)根据对统计图表的分析,请你为沉迷游戏的同学提一个合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9500000000000千米.则“比邻星”距离太阳系约为( )
A. ![]() 千米B.
千米B. ![]() 千米C.
千米C. ![]() 千米D.
千米D. ![]() 千米
千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂加工一种商品,每天加工件数不超过100件时,每件成本80元,每天加工超过100件时,每多加工5件,成本下降2元,但每件成本不得低于70元.设工厂每天加工商品x(件),每件商品成本为y(元),
(1)求出每件成本y(元)与每天加工数量x(件)之间的函数关系式,并注明自变量的取值范围;
(2)若每件商品的利润定为成本的20%,求每天加工多少件商品时利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
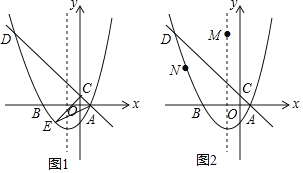
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com