
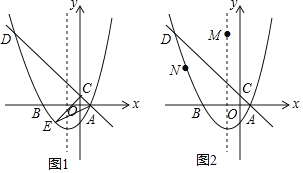
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
【答案】(1)y=x2+2x-3;(2)△ACE的面积的最大值为![]() ;(3)点M的坐标为(-1,26)或(-1,16)或(-1,8).
;(3)点M的坐标为(-1,26)或(-1,16)或(-1,8).
【解析】
(1)先利用抛物线的对称性确定出点B的坐标,然后设抛物线的解析式为y=a(x+3)(x-1),将点D的坐标代入求得a的值即可;
(2)过点E作EF∥y轴,交AD与点F,过点C作CH⊥EF,垂足为H.设点E(m,m2+2m-3),则F(m,-m+1),则EF=-m2-3m+4,然后依据△ACE的面积=△EFA的面积-△EFC的面积列出三角形的面积与m的函数关系式,然后利用二次函数的性质求得△ACE的最大值即可;
(3)当AD为平行四边形的对角线时.设点M的坐标为(-1,a),点N的坐标为(x,y),利用平行四边形对角线互相平分的性质可求得x的值,然后将x=-2代入求得对应的y值,然后依据![]() ,可求得a的值;当AD为平行四边形的边时.设点M的坐标为(-1,a).则点N的坐标为(-6,a+5)或(4,a-5),将点N的坐标代入抛物线的解析式可求得a的值.
,可求得a的值;当AD为平行四边形的边时.设点M的坐标为(-1,a).则点N的坐标为(-6,a+5)或(4,a-5),将点N的坐标代入抛物线的解析式可求得a的值.
(1)∵A(1,0),抛物线的对称轴为x=-1,
∴B(-3,0).
设抛物线的解析式为y=a(x+3)(x-1),
将点D的坐标代入得:5a=5,解得a=1,
∴抛物线的解析式为y=x2+2x-3.
(2)如图1所示:过点E作EF∥y轴,交AD与点F,过点C作CH⊥EF,垂足为H.
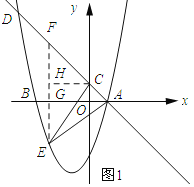
设点E(m,m2+2m-3),则F(m,-m+1).
∴EF=-m+1-m2-2m+3=-m2-3m+4
∴△ACE的面积=△EFA的面积-△EFC的面积=![]() EFAG-
EFAG-![]() EFHC=
EFHC=![]() EFOA=-
EFOA=-![]() (m+
(m+![]() )2+
)2+![]() .
.
∴△ACE的面积的最大值为![]() .
.
(3)当AD为平行四边形的对角线时.
设点M的坐标为(-1,a),点N的坐标为(x,y).
∵平行四边的对角线互相平分,
∴![]() ,
,![]() .
.
解得:x=-2,5-a.
将点N的坐标代入抛物线的解析式得:5-a=-3,
∴a=8.
∴点M的坐标为(/span>-1,8).
当AD为平行四边形的边时.
设点M的坐标为(-1,a).
∵四边形MNAD为平行四边形,
∴点N的坐标为(-6,a+5)或(4,a-5).
∵将x=-6,y=a+5代入抛物线的解析式得:a+5=36-12-3,解得:a=16,
∴M(-1,16).
将x=4,y=a-5代入抛物线的解析式得:a-5=16+8-3,解得:a=26,
∴M(-1,26).
综上所述,当点M的坐标为(-1,26)或(-1,16)或(-1,8)时,以点A,D,M,N为顶点的四边形能成为平行四边形.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
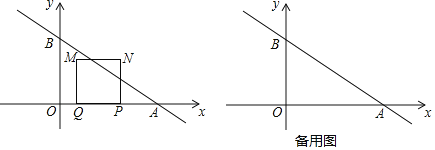
【题目】如图,在平面直角坐标系中,一次函数y=-![]() x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)当正方形PQMN的边MN经过点B时,t= 秒;
(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)连结BN,则BN的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三一次模拟考试后,数学老师把一班的数学成绩制成如图所示不完整的统计图(满分120分,每组含最低分,不含最高分),并给出如下信息:①第二组频率是![]() ;②第二、三组的频率和是
;②第二、三组的频率和是![]() ;③自左至右第三、四、五组的频数比为
;③自左至右第三、四、五组的频数比为![]() .请你结合统计图解答下列问题:
.请你结合统计图解答下列问题:
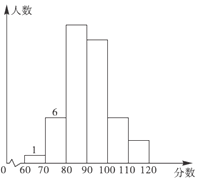
(1)全班学生共有______人,第三组的人数为______人;
(2)如果成绩不少于![]() 分为优秀,那么全年级
分为优秀,那么全年级![]() 人中成绩达到优秀的大约多少人?
人中成绩达到优秀的大约多少人?
(3)若不少于![]() 分的学生可以获得学校颁发的奖状,且每班选派两名代表在学校新学期开学式中领奖,则该班得到
分的学生可以获得学校颁发的奖状,且每班选派两名代表在学校新学期开学式中领奖,则该班得到![]() 分的小强同学能被选中领奖的概率是多少?
分的小强同学能被选中领奖的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
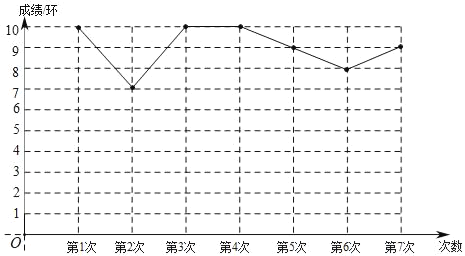
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,…,则等边
,…,则等边![]() 的边长是______.
的边长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
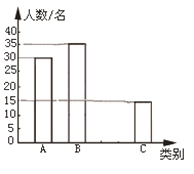
A. 900名 B. 1050名 C. 600名 D. 450名
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.

已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com