
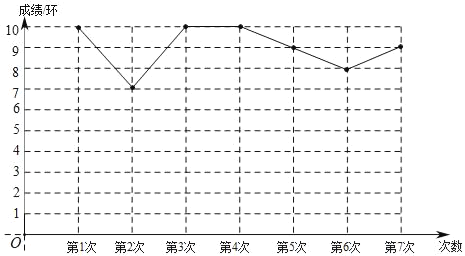
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分) 青少年沉迷于手机游戏,严重危害他们的身心健康,此问题已引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的“王者荣耀”玩家进行了简单的随机抽样调查,绘制出以下两幅统计图.
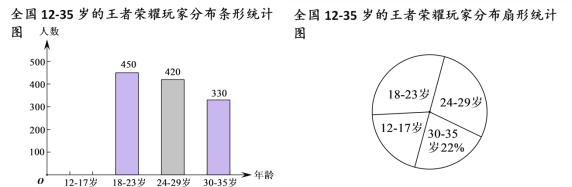
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是_________;
(3)据报道,目前我国12﹣35岁“王者荣耀”玩家的人数约为2000万,请估计其中12﹣23岁的人数.
(4)根据对统计图表的分析,请你为沉迷游戏的同学提一个合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万购买
种型号电脑的数量与用8万购买![]() 种型号电脑的数量相同.
种型号电脑的数量相同.
(1)求![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中![]() 种型号电脑至少要购进10台,请问有哪几种购买方案?
种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
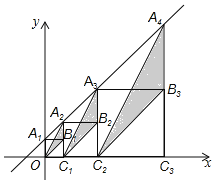
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,按如图方式作正方形
,按如图方式作正方形![]() ,
,![]() ,
,![]() ,…,点
,…,点![]() ,
,![]() ,
,![]() ,…在直线
,…在直线![]() 上,点
上,点![]() ,
,![]() ,
,![]() ,…在
,…在![]() 轴上,图中阴影部分三角形的面积从左到右依次标记为
轴上,图中阴影部分三角形的面积从左到右依次标记为![]() ,
,![]() ,
,![]() ,…,则
,…,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
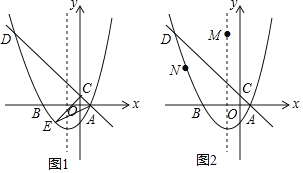
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
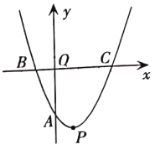
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 点,与
点,与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,且点
两点,且点![]() 在点
在点![]() 的右侧,设抛物线的顶点为
的右侧,设抛物线的顶点为![]() .
.
(1)若点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)当![]() 时,该抛物线上最高点与最低点纵坐标的差为
时,该抛物线上最高点与最低点纵坐标的差为![]() ,求出
,求出![]() 与
与![]() 的关系;若
的关系;若![]() 有最大值或最小值,直接写出这个最大值或最小值.
有最大值或最小值,直接写出这个最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点
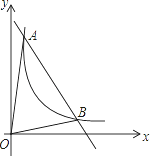
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处“两段式栏杆”如图①所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图②所示,其示意图如图③所示,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2m.现有一高度为2.4m的货车要送货进入地下车库,问此货车能否安全通过?请通过计算说明.(栏杆宽度忽略不计,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
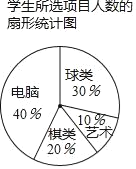
【题目】某校九年(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查,调查项目分别为球类、棋类、电脑、艺术,要求每生必选且只能选其中一类,并根据调查结果列出统计表,绘制成扇形统计图如下:
学生所选项目人数的统计表
项目 | 男生人数 | 女生人数 |
电脑 | a | 8 |
球类 | 8 | b |
棋类 | 4 | c |
艺术 | 2 | 3 |
根据以上信息解决下列问题:
(1)a= ,b= ,c= .
(2)该班要从参加“艺术”课外活动的学生中选2名参加学校艺术节活动,其中有2位女生因有事而弃权,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com