
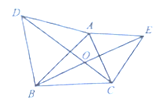
【题目】如图,在![]() 中,分别以
中,分别以![]() ,
,![]() 为边向
为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的度数为:____________________.
的度数为:____________________.
【答案】120゜
【解析】
根据等边三角形证明AB=AD,AC=AE,再利用等式性质得∠DAC=∠BAE,根据SAS得出△ABE≌△ADC,从而得出∠ABE=∠ADC,再根据∠BOC是△BOD的外角,得到∠BOC=∠ODB+∠DBA+∠ABE,据此进行计算即可.
∵△ABD与△ACE均为等边三角形,
∴AD=AB,AC=AE,且∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ABE和△ADC中,
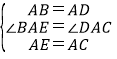 ,
,
∴△ABE≌△ADC(SAS);
∴∠ABE=∠ADC,
∵∠BOC是△BOD的外角,
∴∠BOC=∠ODB+∠DBA+∠ABE
=∠ADC+∠ODB+∠DBA
=∠ADB+∠DBA
=60°+60°
=120°


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队原计划修建一条长100千米的公路,由于实际情况,进行了两次改道,每次改道以相同的百分率增加修路长度,使得实际修建长度为121千米,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍。
(1)求两次改道的平均增长率;
(2)求甲、乙两个工程队每天各修路多少千米?
(3)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过42.4万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
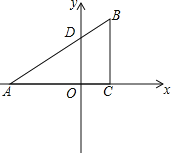
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的横坐标是一元二次方程x2+2x-3=0的两根(AO>OC),直线AB与y轴交于D,D点的坐标为![]()
(1)求直线AB的函数表达式;
(2)在x轴上找一点E,连接EB,使得以点A、E、B为顶点的三角形与△ABC相似(不包括全等),并求点E的坐标;
(3)在(2)的条件下,点P、Q分别是AB和AE上的动点,连接PQ,点P、Q分别从A、E同时出发,以每秒1个单位长度的速度运动,当点P到达点B时,两点停止运动,设运动时间为t秒,问几秒时以点A、P、Q为顶点的三角形与△AEB相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 与点
与点![]() 关于原点对称,一次函数
关于原点对称,一次函数![]() 的图象经过点
的图象经过点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() .
.
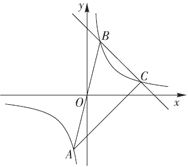
(1)求反比例函数与一次函数的表达式;
(2)求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
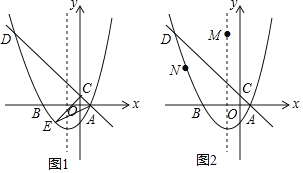
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=40°,点D、点E分别从点B、点C同时出发,在线段BC上作等速运动,到达C点、B点后运动停止.
(1)求证:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度数;
拓展:若△ABD的外心在其内部时,求∠BDA的取值范围.
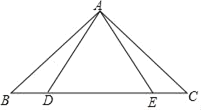
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
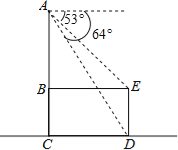
(参考数据:tan53°≈![]() ,sin53°≈
,sin53°≈![]() ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
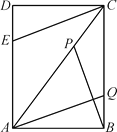
【题目】如图,矩形ABCD中,∠ABC=90,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).
(1)若△CDE与△ADC相似,求t的值.
(2)连接AQ,BP,CE,若BP⊥CE,求t的值;
(3)当PQ长度取得最小值时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com