
ЁОЬтФПЁПМзЁЂввСНИіЙЄГЬЖгдМЦЛЎаоНЈвЛЬѕГЄ100ЧЇУзЕФЙЋТЗЃЌгЩгкЪЕМЪЧщПіЃЌНјааСЫСНДЮИФЕРЃЌУПДЮИФЕРвдЯрЭЌЕФАйЗжТЪдіМгаоТЗГЄЖШЃЌЪЙЕУЪЕМЪаоНЈГЄЖШЮЊ121ЧЇУзЃЌвбжЊМзЙЄГЬЖгУПЬьБШввЙЄГЬЖгУПЬьЖраоТЗ0.5ЧЇУзЃЌввЙЄГЬЖгЕЅЖРЭъГЩаоТЗШЮЮёЫљашЬьЪ§ЪЧМзЙЄГЬЖгЕЅЖРЭъГЩаоТЗШЮЮёЫљашЬьЪ§ЕФ1.5БЖЁЃ
ЃЈ1ЃЉЧѓСНДЮИФЕРЕФЦНОљдіГЄТЪЃЛ
ЃЈ2ЃЉЧѓМзЁЂввСНИіЙЄГЬЖгУПЬьИїаоТЗЖрЩйЧЇУзЃП
ЃЈ3ЃЉШєМзЙЄГЬЖгУПЬьЕФаоТЗЗбгУЮЊ0.5ЭђдЊЃЌввЙЄГЬЖгУПЬьЕФаоТЗЗбгУЮЊ0.4ЭђдЊЃЌвЊЪЙСНИіЙЄГЬЖгаоТЗзмЗбгУВЛГЌЙ§42.4ЭђдЊЃЌМзЙЄГЬЖгжСЩйаоТЗЖрЩйЬьЃП
ЁОД№АИЁПЃЈ1ЃЉСНДЮИФЕРЕФЦНОљдіГЄТЪЮЊ10ЃЅЃЛЃЈ2ЃЉМзЙЄГЬЖгУПЬьаоТЗ1.5ЧЇУзЃЌввЙЄГЬЖгУПЬьаоТЗ1ЧЇУзЃЛЃЈ3ЃЉМзЙЄГЬЖгжСЩйаоТЗ60Ьь.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшСНДЮИФЕРЕФЦНОљдіГЄТЪЮЊxЃЌИљОндМЦЛЎаоТЗЕФГЄЖШМАОСНДЮИФЕРКѓЕФаоТЗГЄЖШЃЌМДПЩЕУГіЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌНтжЎШЁЦфе§жЕМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЩшввЙЄГЬЖгУПЬьаоТЗyЧЇУзЃЌдђМзЙЄГЬЖгУПЬьаоТЗЃЈy+0.5ЃЉЧЇУзЃЌИљОнЙЄзїЪБМф=ЙЄзїзмСПЁТЙЄзїаЇТЪНсКЯввЙЄГЬЖгЕЅЖРЭъГЩаоТЗШЮЮёЫљашЬьЪ§ЪЧМзЙЄГЬЖгЕЅЖРЭъГЩаоТЗШЮЮёЫљашЬьЪ§ЕФ1.5БЖЃЌМДПЩЕУГіЙигкyЕФЗжЪНЗНГЬЃЌНтжЎОМьбщКѓМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЩшМзЙЄГЬЖгаоТЗmЬьЃЌдђввЙЄГЬЖгаоТЗЃЈ121-1.5mЃЉЬьЃЌИљОнзмЗбгУ=МзЙЄГЬЖгУПШеЫљашЗбгУЁСМзЙЄГЬЖгЙЄзїЬьЪ§+ввЙЄГЬЖгУПШеЫљашЗбгУЁСввЙЄГЬЖгЙЄзїЬьЪ§НсКЯСНИіЙЄГЬЖгаоТЗзмЗбгУВЛГЌЙ§42.4ЭђдЊЃЌМДПЩЕУГіЙигкmЕФвЛдЊвЛДЮВЛЕШЪНЃЌНтжЎШЁЦфжаЕФзюаЁжЕМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЩшСНДЮИФЕРЕФЦНОљдіГЄТЪЮЊ![]() ЃЌ
ЃЌ
вРЬтвтЕУЃК![]()
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЙЪСНДЮИФЕРЕФЦНОљдіГЄТЪЮЊ10ЃЅЃЛ
ЃЈ2ЃЉЩшввЙЄГЬЖгУПЬьаоТЗ![]() ЧЇУзЃЌМзЙЄГЬЖгУПЬьаоТЗ
ЧЇУзЃЌМзЙЄГЬЖгУПЬьаоТЗ![]() ЧЇУзЃЌ
ЧЇУзЃЌ
ИљОнЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ОМьбщЃК![]() ЪЧЗНГЬЕФНтЃЌ
ЪЧЗНГЬЕФНтЃЌ
![]() ЃЈЧЇУзЃЉ
ЃЈЧЇУзЃЉ
Д№ЃКМзЙЄГЬЖгУПЬьаоТЗ1.5ЧЇУзЃЌввЙЄГЬЖгУПЬьаоТЗ1ЧЇУзЃЛ
ЃЈ3ЃЉЩшМзЙЄГЬЖгаоТЗ![]() ЬьЃЌ
ЬьЃЌ
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКМзЙЄГЬЖгжСЩйаоТЗ60Ьь.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЈ
ЃЈ![]() дк
дк![]() ЕФзѓВрЃЉЃЌНЛ
ЕФзѓВрЃЉЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌЙ§Еу
ЩЯвЛЕуЃЌЙ§Еу![]() зї
зї![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() . ЩшЕу
. ЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() .
.
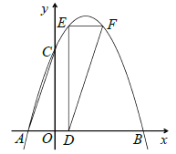
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ2ЃЉСЌНс![]() ЃЌЕБ
ЃЌЕБ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
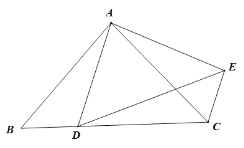
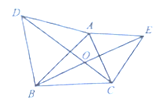
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC,DЪЧBCЩЯШЮвЛЕуЃЌAD=AEЧвЁЯBAC=ЁЯDAE.
ЃЈ1ЃЉШєEDЦНЗжЁЯAEC,ЧѓжЄЃКCEЁЮADЃЛ
ЃЈ2ЃЉШєЁЯBAC=90ЁуЃЌЧвDдкBCжаЕуЪБЃЌЪдХаЖЯЫФБпаЮADCEЕФаЮзДЃЌВЂЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+cЕФЖдГЦжсЪЧжБЯпxЃН1ЃЌЧвОЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌдђЯТСаНсТлЃКЂйabcЃМ0ЃЛЂк2aЉbЃН0ЃЛЂлaЃМЉ![]() ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
ЃЛЂмШєЗНГЬax2+bx+cЉ2ЃН0ЕФСНИіИљЮЊx1КЭx2ЃЌдђЃЈx1+1ЃЉЃЈx2Љ3ЃЉЃМ0ЃЌе§ШЗЕФгаЃЈЁЁЁЁЃЉИіЃЎ
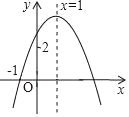
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
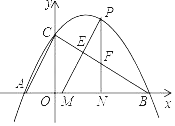
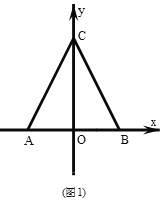
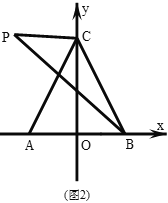
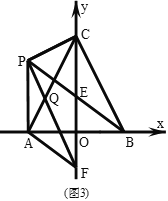
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+![]() ЕФЭМЯѓОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсЯрНЛгкЕуCЃЎЕуPЮЊЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPЗжБ№зіBCКЭxжсЕФДЙЯпЃЌНЛBCгкЕуEКЭFЃЌНЛxжсгкЕуMКЭNЃЎ
ЕФЭМЯѓОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгыyжсЯрНЛгкЕуCЃЎЕуPЮЊЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPЗжБ№зіBCКЭxжсЕФДЙЯпЃЌНЛBCгкЕуEКЭFЃЌНЛxжсгкЕуMКЭNЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЯпЖЮPEзюДѓжЕЃЌВЂЧѓГіЯпЖЮPEзюДѓЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєSЁїPMNЃН3SЁїPEFЪБЃЌЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌвбжЊЁїABCЕФжмГЄЮЊ15ЃЌдђСтаЮ
ЃЌвбжЊЁїABCЕФжмГЄЮЊ15ЃЌдђСтаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЕФГЄЮЊ( ).
ЕФГЄЮЊ( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЮЊзјБъдЕуЃЌжБЯп
ЮЊзјБъдЕуЃЌжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсИКАыжсКЭ
жсИКАыжсКЭ![]() жсе§Аыжсгк
жсе§Аыжсгк![]() СНЕуЃЌНЋ
СНЕуЃЌНЋ![]() би
би![]() жсЗелжС
жсЗелжС![]() ЃЌЧв
ЃЌЧв![]() ЕФУцЛ§ЮЊ8.
ЕФУцЛ§ЮЊ8.
(1)ШчЭМЃЌЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
(2)ШчЭМЃЌЕу![]() ЮЊЕкЖўЯѓЯоФк
ЮЊЕкЖўЯѓЯоФк![]() ЩЯЗНЕФвЛЕуЃЌСЌНг
ЩЯЗНЕФвЛЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪН(гУКЌ
ЕФКЏЪ§ЙиЯЕЪН(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
(3)ШчЭМЃЌдк(2)ЕФЬѕМўЯТЃЌСЌНг![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() жсИКАыжсЩЯвЛЕуЃЌ
жсИКАыжсЩЯвЛЕуЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() зјБъ.
зјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЗжБ№вд
жаЃЌЗжБ№вд![]() ЃЌ
ЃЌ![]() ЮЊБпЯђ
ЮЊБпЯђ![]() ЭтзїЕШБп
ЭтзїЕШБп![]() КЭЕШБп
КЭЕШБп![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФЖШЪ§ЮЊЃК____________________.
ЕФЖШЪ§ЮЊЃК____________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
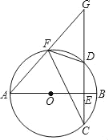
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкЕуEЃЌFЪЧЛЁADЩЯЕФвЛЕуЃЌAFЃЌCDЕФбгГЄЯпЯрНЛгкЕуGЃЎ
ЃЈ1ЃЉШєЁбOЕФАыОЖЮЊ3![]() ЃЌЧвЁЯDFCЃН45ЁуЃЌЧѓЯвCDЕФГЄЃЎ
ЃЌЧвЁЯDFCЃН45ЁуЃЌЧѓЯвCDЕФГЄЃЎ
ЃЈ2ЃЉЧѓжЄЃКЁЯAFCЃНЁЯDFGЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com