
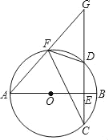
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是弧AD上的一点,AF,CD的延长线相交于点G.
(1)若⊙O的半径为3![]() ,且∠DFC=45°,求弦CD的长.
,且∠DFC=45°,求弦CD的长.
(2)求证:∠AFC=∠DFG.
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队原计划修建一条长100千米的公路,由于实际情况,进行了两次改道,每次改道以相同的百分率增加修路长度,使得实际修建长度为121千米,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍。
(1)求两次改道的平均增长率;
(2)求甲、乙两个工程队每天各修路多少千米?
(3)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过42.4万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
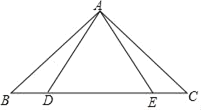
【题目】如图,在△ABC中,∠B=∠C=40°,点D、点E分别从点B、点C同时出发,在线段BC上作等速运动,到达C点、B点后运动停止.
(1)求证:△ABE≌△ACD;
(2)若AB=BE,求∠DAE的度数;
拓展:若△ABD的外心在其内部时,求∠BDA的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
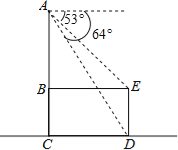
(参考数据:tan53°≈![]() ,sin53°≈
,sin53°≈![]() ,tan64°≈2,sin64°≈
,tan64°≈2,sin64°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() 图象上一点,过点A作x轴的平行线交反比例函数y=﹣
图象上一点,过点A作x轴的平行线交反比例函数y=﹣![]() 的图象于点B,点C在x轴上,且S△ABC=
的图象于点B,点C在x轴上,且S△ABC=![]() ,则k=( )
,则k=( )
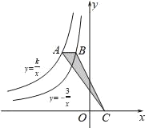
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是______.
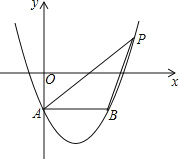
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABC=90,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).
(1)若△CDE与△ADC相似,求t的值.
(2)连接AQ,BP,CE,若BP⊥CE,求t的值;
(3)当PQ长度取得最小值时,求t的值.
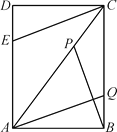
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,交y轴于点
,交y轴于点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线解析式;
(2)在第一象限内的抛物线上求点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)![]() 是第一象限内抛物线上一点,
是第一象限内抛物线上一点,![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 在
在![]() 点右侧,且满足
点右侧,且满足![]() ,当
,当![]() 为何值时,满足条件的点
为何值时,满足条件的点![]() 只有一个?
只有一个?
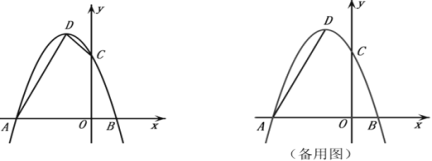
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com