
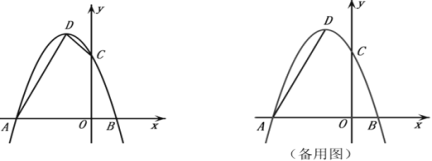
【题目】已知抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,交y轴于点
,交y轴于点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线解析式;
(2)在第一象限内的抛物线上求点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)![]() 是第一象限内抛物线上一点,
是第一象限内抛物线上一点,![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 在
在![]() 点右侧,且满足
点右侧,且满足![]() ,当
,当![]() 为何值时,满足条件的点
为何值时,满足条件的点![]() 只有一个?
只有一个?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)已知抛物线过定点,用待定系数法即可求解;(2)过点D作DH⊥y轴交y轴于点H,DH=HC,OA=OC,∠DHC=∠AOC=90°得△DHC和△AOC都是等腰直角三角形,从而得出∠DCH=∠ACO=45°,DC=![]() ,AC=
,AC=![]() ,∠ACD=90°,DC⊥AC,延长DC至N使CN=DC=
,∠ACD=90°,DC⊥AC,延长DC至N使CN=DC=![]() ,根据
,根据![]() ,
,![]() ,得出S△ADC=S△ACM,得出直线AC的解析式为:y=x+3,从而得出直线NM的解析式为:y=x+1,由
,得出S△ADC=S△ACM,得出直线AC的解析式为:y=x+3,从而得出直线NM的解析式为:y=x+1,由![]() 求得点M的坐标为:
求得点M的坐标为:![]() ;(3)延长DF交x轴于点E,过点D作DG⊥x轴交x轴于点G,设OE=a,则EA=ED=a+3,GE=a+1,在Rt△DGE中,DG2+GE2=DE2,解得a=2,解得E(2,0)得直线DE的解析式为:
;(3)延长DF交x轴于点E,过点D作DG⊥x轴交x轴于点G,设OE=a,则EA=ED=a+3,GE=a+1,在Rt△DGE中,DG2+GE2=DE2,解得a=2,解得E(2,0)得直线DE的解析式为:![]() ,联立
,联立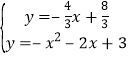 ,由此可得
,由此可得![]() ,由∠APF是△DPF的一个外角,可得△FDP≌△PAQ,
,由∠APF是△DPF的一个外角,可得△FDP≌△PAQ,![]() ,易得
,易得![]() ,
,![]() ,,设DP=x,则PA=
,,设DP=x,则PA=![]() ,则AQ=m+3,由
,则AQ=m+3,由![]() ,整理得
,整理得![]() ,令△=0,解得
,令△=0,解得![]() .
.
(1)依题有![]()
解得,![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
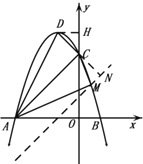
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
由(1)得,![]()
![]() ,
,![]() ,
,
又![]() ,
,
![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
延长![]() 至
至![]() 使
使![]() ,
,
易得![]()
过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
依题有![]() 的解析式为:
的解析式为:![]() ,
,
设![]() 的解析式为:
的解析式为:![]()
将点![]() 代入
代入![]() 的解析式得,
的解析式得,![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
联立![]()
解得,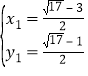 ,
, 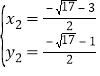 (舍去)
(舍去)
![]() ;
;
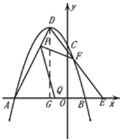
(3)如图,延长![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]()
![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]()
即![]() ,解得,
,解得,![]() .
.
![]()
![]() 直线的解析式为:
直线的解析式为:![]()
联立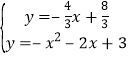
解得: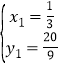 ,
,![]() ,
,
![]() 是第一象限内抛物线上一点,
是第一象限内抛物线上一点,
![]()
![]() 是
是![]() 的一个外角,
的一个外角,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
易得,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
依题有![]() ,
,
![]() ,
,
![]() ,
,
整理得,![]() ,
,
![]() .
.
∵当![]() 时,满足条件的
时,满足条件的![]() 只有一个,
只有一个,
![]() ,
,
解得,![]() .
.


科目:初中数学 来源: 题型:
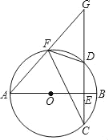
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是弧AD上的一点,AF,CD的延长线相交于点G.
(1)若⊙O的半径为3![]() ,且∠DFC=45°,求弦CD的长.
,且∠DFC=45°,求弦CD的长.
(2)求证:∠AFC=∠DFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
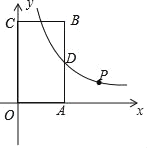
【题目】如图,矩形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,点B的坐标为(4,m)(5≤m≤7),反比例函数y=![]() (x>0)的图象交边AB于点D.
(x>0)的图象交边AB于点D.
(1)用m的代数式表示BD的长;
(2)设点P在该函数图象上,且它的横坐标为m,连结PB,PD
①记矩形OABC面积与△PBD面积之差为S,求当m为何值时,S取到最大值;
②将点D绕点P逆时针旋转90°得到点E,当点E恰好落在x轴上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
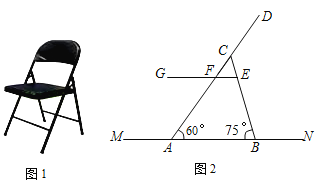
【题目】如图1是一把折叠椅子,如图2是椅子完全打开支稳后的侧面示意图,![]() 表示地面所在的直线,其中
表示地面所在的直线,其中![]() 和
和![]() 表示两根较粗的钢管,
表示两根较粗的钢管,![]() 表示座板平面,
表示座板平面,![]() ,交
,交![]() 于点F,且
于点F,且![]() ,
,![]() 长
长![]() ,
,![]() ,
,![]() 长24cm,
长24cm,![]() 长24cm,
长24cm,
(1)求座板![]() 的长;
的长;
(2)求此时椅子的最大高度(即点D到直线![]() 的距离).(结果保留根号)
的距离).(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
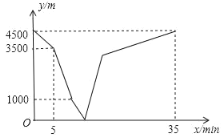
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=![]() 交x轴于点A、B(点A在点B的左侧),交y轴于点C.
交x轴于点A、B(点A在点B的左侧),交y轴于点C.
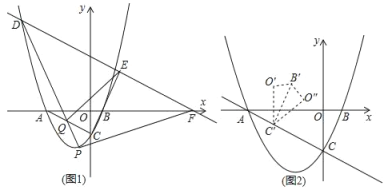
(1)如图,点D是抛物线在第二象限内的一点,且满足|xD﹣xA|=2![]() ,过点D作AC的平行线,分别与x轴、射线CB交于点F、E,点P为直线AC下方抛物线上的一动点,连接PD交线段AC于点Q,当四边形PQEF的面积最大时,在y轴上找一点M,x轴上找一点N,使得PM+MN﹣
,过点D作AC的平行线,分别与x轴、射线CB交于点F、E,点P为直线AC下方抛物线上的一动点,连接PD交线段AC于点Q,当四边形PQEF的面积最大时,在y轴上找一点M,x轴上找一点N,使得PM+MN﹣![]() NB取得最小值,求这个最小值;
NB取得最小值,求这个最小值;
(2)如图2,将△BOC沿着直线AC平移得到△B′O′C′,再将△B'O′C′沿B′C′翻折得到△B′O″C′,连接BC′、O″B,则△C′BO″能否构成等腰三角形?若能,请直接写出所有符合条件的点O″的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:
请解答下列问题:
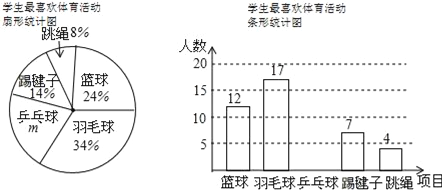
(1)m= %,这次共抽取了 名学生进行调查;请补全条形统计图;
(2)若全校有800名学生,则该校约有多少名学生喜爱打篮球?
(3)学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com