
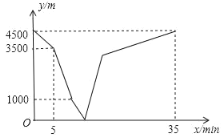
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
【答案】1500.
【解析】
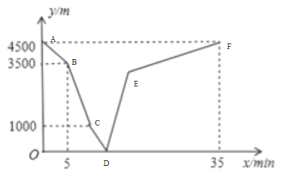
分析图象:点A表示出发前两人相距4500米,即家和图书馆相距4500米;线段AB表示小雪已跑步出发,两人相距距离逐渐减小,到5分钟时相距3500米,即小雪5分钟走了1000米,可求小雪跑步的速度;线段BC表示小松5分钟后开始出发;点C表示两人相距1000米时,小雪改为步行,可设小雪跑步a分钟,则后面(35﹣a)分钟步行,列方程可求出a,然后用4500减1000再减去小雪走的路程可求出此时小松骑车走的路程,即求出小松的速度;点D表示两人相遇;线段DE表示两人相遇后继续往前走,点E表示小松到达家,可用路程除以小松的速度得到此时为第几分钟;线段EF表示小雪继续往图书馆走;点F表示35分钟时小雪到达图书馆.
由图象可得:家和图书馆相距4500米,小雪的跑步速度为:(4500﹣3500)÷5=200(米/分钟),
∴小雪步行的速度为:200×![]() =100(米/分钟),
=100(米/分钟),
设小雪在第a分钟时改为步行,列方程得:
200a+100(35﹣a)=4500
解得:a=10
∴小松骑车速度为:(4500﹣200×10﹣1000)÷(10﹣5)=300(米/分钟)
∴小松到家时的时间为第:4500÷300+5=20(分钟)
此时小雪离图书馆还有15分钟路程,100×15=1500(米)
故答案为1500.


科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
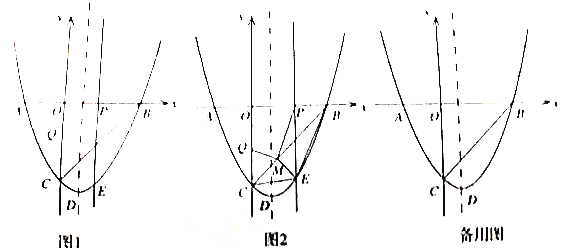
【题目】如图,抛物线![]() 与x轴分别交于点
与x轴分别交于点![]() ,与y轴交于点C,顶点为D.
,与y轴交于点C,顶点为D.
(1)求抛物线的解析式和顶点D的坐标;
(2)动点![]() 以相同的速度从点O同时出发,分别在线段
以相同的速度从点O同时出发,分别在线段![]() 上向点
上向点![]() 方向运动,过点P作x轴的垂线,交抛物线于点E.
方向运动,过点P作x轴的垂线,交抛物线于点E.
①当四边形![]() 为矩形时,求点E的坐标;
为矩形时,求点E的坐标;
②过点E作![]() 于点M,连接
于点M,连接![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,当
,当![]() 将
将![]() 的面积分成1:3两部分时,请直接写出的
的面积分成1:3两部分时,请直接写出的![]() 值;
值;
③连接![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
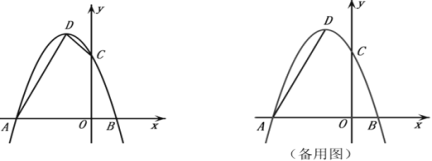
【题目】已知抛物线![]() 过点
过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,交y轴于点
,交y轴于点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线解析式;
(2)在第一象限内的抛物线上求点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)![]() 是第一象限内抛物线上一点,
是第一象限内抛物线上一点,![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 在
在![]() 点右侧,且满足
点右侧,且满足![]() ,当
,当![]() 为何值时,满足条件的点
为何值时,满足条件的点![]() 只有一个?
只有一个?
查看答案和解析>>
科目:初中数学 来源: 题型:
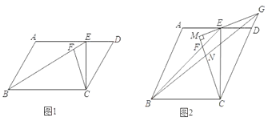
【题目】如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=BF=4,DC=2,求EF的长;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N,若CM=MG,求证:EG=2MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.
(1)用画树状图或列表等方法列出所有可能出现的结果;
(2)求点A落在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
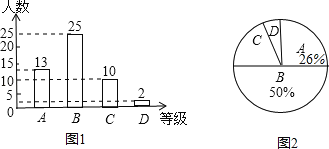
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若AB=8cm,BC=4cm,求四边形DEBF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com