
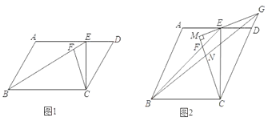
【题目】如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=BF=4,DC=2,求EF的长;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N,若CM=MG,求证:EG=2MN.
【答案】(1)EF=![]() ﹣4;(2)证明见解析.
﹣4;(2)证明见解析.
【解析】
(1)利用勾股定理求出EC,BE即可解决问题.
(2)如图2中,延长GM到H,使得MH=MG,连接CH,BH.想办法证明EG=BH,BH=2MN即可解决问题.
(1)解:如图1中,
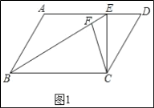
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EC⊥BC,
∴AD⊥EC,
∴∠BCE=∠CED=90°,
∵∠ECD=30°,CD=2,
∴CE=CDcos30°=![]() ,
,
在Rt△BCE中,BE=![]() =
=![]() ,
,
∵BC=CF=4,
∴EF=BE﹣BF=![]() -4.
-4.
(2)证明:如图2中,延长GM到H,使得MH=MG,连接CH,BH.
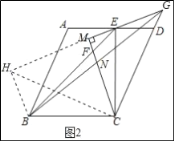
∵CM=MG=MH,CM⊥GH,
∴∠HCG=90°,CH=CG,
∴∠HCG=∠BCE,
∴∠BCH=∠ECG,
∵CB=CE,
∴△BCH≌△ECG(SAS),
∴BH=EG,∠CHB=∠CGE=45°,
∵∠CHG=45°,
∴∠BHG=90°,
∴∠BHG=∠CMG=90°,
∴MN∥BH,∵HM=HG,
∴BN=NG,
∴BH=2MN,
∴EG=2MN.


科目:初中数学 来源: 题型:
【题目】如图1中,△ABC为等腰三角形,AB=AC,点E为腰AB上任意一点,以CE为底边作等腰△DEC.且∠BAC=∠EDC=α,连结AD:
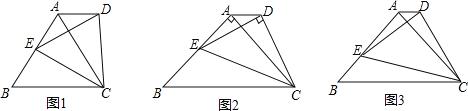
(1)如图2中,当α=60°时,∠DAC=______,![]() =______;
=______;
(2)如图3中,当α=90°时,求∠DAC的度数与![]() 的值;
的值;
(3)如图1中,当BC=![]() AC.∠DAC=___(用α的代数式表示)
AC.∠DAC=___(用α的代数式表示)![]() =___.
=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
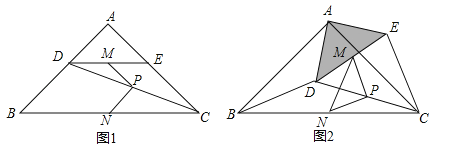
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生小亮响应国家创新创业号召,回家乡承包了一片坡地,改造后种植优质猕猴桃.经核算这批猕猴桃的种植成本为16 元![]() ,设销售时间为
,设销售时间为![]() (天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元
(天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元![]() )与时间x(天)的关系:当
)与时间x(天)的关系:当![]() 时,p与x满足一次函数关系,如下表:
时,p与x满足一次函数关系,如下表:
| 2 | 4 | 6 | ...... |
| 35 | 34 | 33 | ...... |
当![]() 时,销售价格稳定为24元
时,销售价格稳定为24元![]() ;②猕猴桃的销售量
;②猕猴桃的销售量![]() 与时间
与时间![]() (天)之间的关系:第一天卖出
(天)之间的关系:第一天卖出![]() ,以后每天比前一天多卖出
,以后每天比前一天多卖出![]() .
.
(1)填空:试销的一个月中,销售价p(元![]() )与时间
)与时间![]() (天)的函数关系式为____;销售量
(天)的函数关系式为____;销售量![]() 与时间x(天)的函数关系式为_____.
与时间x(天)的函数关系式为_____.
2)求销售第几天时,当天的利润最大?最大利润是多少?
(3)请求出试销的一个月中当天销售利润不低于 930 元的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
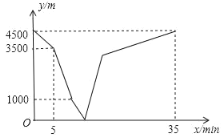
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
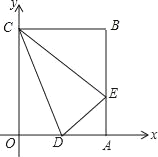
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点M为二次函数y=﹣x2+2bx+1+4b﹣b2图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否恒在某条直线上?若是,求出该直线解析式;若不是,说明理由.
(2)若二次函数图象也经过点A,B,且mx+5>﹣x2+2bx+2+4b﹣b2,借助图象,求出x的取值范围.
(3)点A坐标为(5,0),点M在△AOB内时,若点C(![]() ,y1),D(
,y1),D(![]() ,y2)都在二次函数图象上,试比较y1与y2的大小.
,y2)都在二次函数图象上,试比较y1与y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com