
【题目】如图1中,△ABC为等腰三角形,AB=AC,点E为腰AB上任意一点,以CE为底边作等腰△DEC.且∠BAC=∠EDC=α,连结AD:
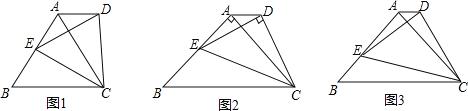
(1)如图2中,当α=60°时,∠DAC=______,![]() =______;
=______;
(2)如图3中,当α=90°时,求∠DAC的度数与![]() 的值;
的值;
(3)如图1中,当BC=![]() AC.∠DAC=___(用α的代数式表示)
AC.∠DAC=___(用α的代数式表示)![]() =___.
=___.
【答案】(1)60°,1;(2)∠DAC=45°,![]() =
=![]() (3)180°-2α,
(3)180°-2α,![]() .
.
【解析】
(1)由三角形ABC与三角形CDE都为正三角形,得到AB=AC,CE=CD,以及内角为60°,利用等式的性质得到∠ECB=∠DCA,利用SAS得到三角形ECB与三角形DCA全等,利用全等三角形对应边相等得到BE=AD,即可求出所求之比;
(2)由三角形CDE与三角形ABC都为等腰直角三角形,利用等腰直角三角形的性质得到CE=![]() CD,BC=
CD,BC=![]() AC,以及锐角为45°,利用等式的性质得到∠ECB=∠DCA,利用两边对应成比例且夹角相等的三角形相似得到三角形ECB与三角形DCA相似,利用相似三角形对应边成比例即可求出所求之比;
AC,以及锐角为45°,利用等式的性质得到∠ECB=∠DCA,利用两边对应成比例且夹角相等的三角形相似得到三角形ECB与三角形DCA相似,利用相似三角形对应边成比例即可求出所求之比;
(3)仿照前两问,以此类推得到一般性规律,求出所求之比即可.
解:(1)∵△ABC和△CDE都是正三角形,
∴∠B=∠ACB=∠DCE=60°,AB=AC,CE=DC,
∵∠ECB=∠ACB-∠ACE=60°-∠ACE,
∠DCA=∠DCE-∠ACE=60°-∠ACE,
∴∠ECB=∠DCA,
在△ECB和△DCA中,
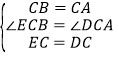 ,
,
∴△ECB≌△DCA(SAS),
∴BE=AD,∠B=∠DAC=60°,
则![]() =1;
=1;
故答案为:60°;1;
(2)∵等腰Rt△ABC和等腰Rt△CDE中,
∴∠B=∠ACB=∠DCE=45°,CE=![]() DC,BC=
DC,BC=![]() AC,
AC,
∴![]() ,
,
∵∠ECB=∠ACB-∠ACE=45°-∠ACE,
∠ACD=∠DCE-∠ACE=45°-∠ACE,
∴∠ECB=∠DCA,
∴△ECB∽△DCA,
∴∠B=∠DAC=45°,
∴![]() ;
;
(3)依此类推,当BC=![]() AC时,
AC时,![]() ,理由为:
,理由为:
∵等腰△ABC和等腰△CDE中,
∴∠B=∠ACB=∠DCE,CE=![]() DC,BC=
DC,BC=![]() AC,
AC,
∴![]() ,
,
∵∠ECB=∠ACB-∠ACE,∠ACD=∠DCE-∠ACE,
∴∠ECB=∠DCA,
∴△ECB∽△DCA,
∴∠B=∠DAC=180°-2α,
∴![]() .
.
故答案为:180°-2α;![]() .
.


科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万购买
种型号电脑的数量与用8万购买![]() 种型号电脑的数量相同.
种型号电脑的数量相同.
(1)求![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中![]() 种型号电脑至少要购进10台,请问有哪几种购买方案?
种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点
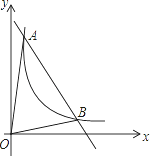
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处“两段式栏杆”如图①所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆经过时,栏杆AEF升起后的位置如图②所示,其示意图如图③所示,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2m.现有一高度为2.4m的货车要送货进入地下车库,问此货车能否安全通过?请通过计算说明.(栏杆宽度忽略不计,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对边相等而另一组对边不相等的凸四边形叫做“等对边四边形”.
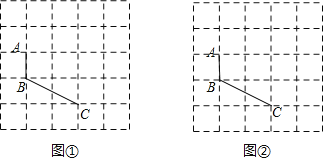
(1)已知:图①、图②是5×5的正方形网格,线段AB、BC的端点均在格点上.在图①、图②中,按要求以AB、BC为边各画一个等对边四边形ABCD.
要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.
(2)若每个小正方形网格的边长为一个单位,请直接写出(1)问中所画每个等对边四边形ABCD的面积______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
①∠PAD=∠PDA=60; ②△PAO≌△ADE;③PO=![]() r;④AO∶OP∶PA=1∶
r;④AO∶OP∶PA=1∶![]() ∶
∶![]() .
.
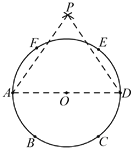
A. ①④B. ②③C. ③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
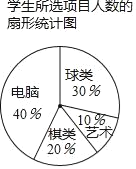
【题目】某校九年(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查,调查项目分别为球类、棋类、电脑、艺术,要求每生必选且只能选其中一类,并根据调查结果列出统计表,绘制成扇形统计图如下:
学生所选项目人数的统计表
项目 | 男生人数 | 女生人数 |
电脑 | a | 8 |
球类 | 8 | b |
棋类 | 4 | c |
艺术 | 2 | 3 |
根据以上信息解决下列问题:
(1)a= ,b= ,c= .
(2)该班要从参加“艺术”课外活动的学生中选2名参加学校艺术节活动,其中有2位女生因有事而弃权,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
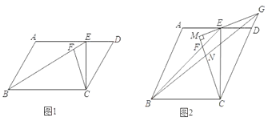
【题目】如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=BF=4,DC=2,求EF的长;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N,若CM=MG,求证:EG=2MN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com