
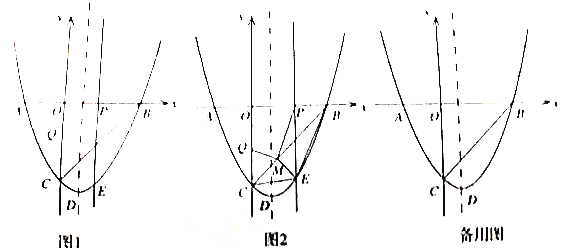
【题目】如图,抛物线![]() 与x轴分别交于点
与x轴分别交于点![]() ,与y轴交于点C,顶点为D.
,与y轴交于点C,顶点为D.
(1)求抛物线的解析式和顶点D的坐标;
(2)动点![]() 以相同的速度从点O同时出发,分别在线段
以相同的速度从点O同时出发,分别在线段![]() 上向点
上向点![]() 方向运动,过点P作x轴的垂线,交抛物线于点E.
方向运动,过点P作x轴的垂线,交抛物线于点E.
①当四边形![]() 为矩形时,求点E的坐标;
为矩形时,求点E的坐标;
②过点E作![]() 于点M,连接
于点M,连接![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,当
,当![]() 将
将![]() 的面积分成1:3两部分时,请直接写出的
的面积分成1:3两部分时,请直接写出的![]() 值;
值;
③连接![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;(2)①
;(2)①![]() ;②15或
;②15或![]() ;③
;③![]()
【解析】
(1)将点A、B代入抛物线解析式即可,则点D坐标可求.
(2)①四边形为矩形,可分析出OQ=PE,设点坐标表示线段长度列式求解即可.
②PE分三角形的面积之比为1:3,可分析出PE分线段BC为1:3,分两种情况讨论,分别求出S1和S2,则比值可求.
③转化线段CP为线段BQ,作点D关于y轴的对称点,连接BD′,与y轴的交点即为点Q,求出BD′的长度就是CP+DQ的最小值.
解:(1)将点A、B代入解析式
![]()
解得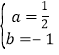 ,
,
∴y=![]() -x-4
-x-4
当x=1时,y=-![]() ,
,
∴D(1,-![]() ).
).
(2)①设点E的坐标为(m,![]() -m-4),则点P(m,0),点Q(0,-m),
-m-4),则点P(m,0),点Q(0,-m),
∵四边形OQEP为矩形,
∴OQ=EP,
∴m=-![]() +m+4,
+m+4,
解得![]() =-2
=-2![]() (舍去),m2=2
(舍去),m2=2![]() .
.
∴E(2![]() , -2
, -2![]()
②令x=0,y=-4,
∴C(0,-4),
∵PE将△BCE的面积分成1:3两部分,
∴PE将线段BC分成1:3两部分,
情况一:当PE过靠近点C的四等分点时,点P的坐标为(1,0),点E(1,-![]() ),
),
∴点Q(0,-1),
直线BC的解析式为y=x-4,
当x=1时,y=-3,
∴点G(1,-3),
如图1所示,

∴GD=![]() ,
,
∵∠CGD=∠OBC=45°,
∴xM=1-![]() ,
,
∴M(![]() ),
),
∴S1=3![]()
![]() =
=![]() , S2=3
, S2=3![]()
![]() =
=![]() ,
,
∴![]() =15.
=15.
情况二:当PE过靠近点B的四等分点时,点P(3,0),点Q(0,-3),点E(3,-![]() ),点G(3,-1),
),点G(3,-1),
∴EG=![]() ,
,
∴xM=3-![]() ,
,
∴M(![]() ,-
,-![]() ),
),
∴S1=1![]()
![]() =
=![]() , S2=1
, S2=1![]()
![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
综上所述:![]() =15或
=15或![]() =
=![]() .
.
③如图2所示,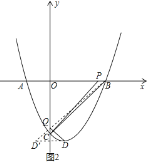
∵OP=OQ,∠BOQ=∠COP,OB=OC,
∴△BOQ≌△COP(SAS),
∴CP=BQ,
∴CP+DQ=BQ+DQ,
作点D关于y轴的对称点D′(-1,-![]() ),
),
连接BD′,与y轴的交点即为点Q,
BD′=![]() =
=![]() .
.
∴CP+DQ的最小值为![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
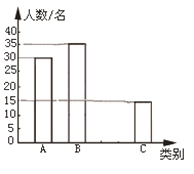
A. 900名 B. 1050名 C. 600名 D. 450名
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.

已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
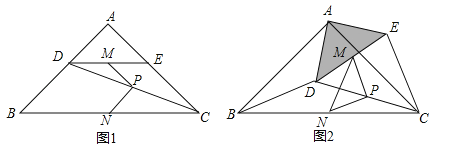
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
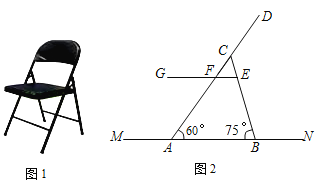
【题目】如图1是一把折叠椅子,如图2是椅子完全打开支稳后的侧面示意图,![]() 表示地面所在的直线,其中
表示地面所在的直线,其中![]() 和
和![]() 表示两根较粗的钢管,
表示两根较粗的钢管,![]() 表示座板平面,
表示座板平面,![]() ,交
,交![]() 于点F,且
于点F,且![]() ,
,![]() 长
长![]() ,
,![]() ,
,![]() 长24cm,
长24cm,![]() 长24cm,
长24cm,
(1)求座板![]() 的长;
的长;
(2)求此时椅子的最大高度(即点D到直线![]() 的距离).(结果保留根号)
的距离).(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生小亮响应国家创新创业号召,回家乡承包了一片坡地,改造后种植优质猕猴桃.经核算这批猕猴桃的种植成本为16 元![]() ,设销售时间为
,设销售时间为![]() (天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元
(天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元![]() )与时间x(天)的关系:当
)与时间x(天)的关系:当![]() 时,p与x满足一次函数关系,如下表:
时,p与x满足一次函数关系,如下表:
| 2 | 4 | 6 | ...... |
| 35 | 34 | 33 | ...... |
当![]() 时,销售价格稳定为24元
时,销售价格稳定为24元![]() ;②猕猴桃的销售量
;②猕猴桃的销售量![]() 与时间
与时间![]() (天)之间的关系:第一天卖出
(天)之间的关系:第一天卖出![]() ,以后每天比前一天多卖出
,以后每天比前一天多卖出![]() .
.
(1)填空:试销的一个月中,销售价p(元![]() )与时间
)与时间![]() (天)的函数关系式为____;销售量
(天)的函数关系式为____;销售量![]() 与时间x(天)的函数关系式为_____.
与时间x(天)的函数关系式为_____.
2)求销售第几天时,当天的利润最大?最大利润是多少?
(3)请求出试销的一个月中当天销售利润不低于 930 元的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
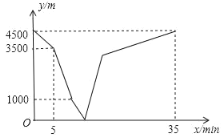
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
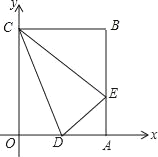
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com