
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【答案】(1)清理养鱼网箱的人均费用为2000元,清理捕鱼网箱的人均费用为3000元;(2)分配清理人员方案有两种:方案一:18人清理养鱼网箱,22人清理捕鱼网箱;方案二:19人清理养鱼网箱,21人清理捕鱼网箱.
【解析】
(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,根据A、B两村庄总支出列出关于x、y的方程组,解之可得;
(2)设m人清理养鱼网箱,则(40﹣m)人清理捕鱼网箱,根据“总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数”列不等式组求解可得.
(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:清理养鱼网箱的人均费用为2000元,清理捕鱼网箱的人均费用为3000元;
(2)设m人清理养鱼网箱,则(40﹣m)人清理捕鱼网箱,
根据题意,得:![]() ,
,
解得:18≤m<20,
∵m为整数,
∴m=18或m=19,
则分配清理人员方案有两种:
方案一:18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:19人清理养鱼网箱,21人清理捕鱼网箱.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1
(2)点C1的坐标为_________,△ABC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为 . 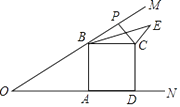
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.

根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是________米
(2)小明在书店停留了___________分钟.
(3)本次上学途中,小明一共行驶了________ 米,一共用了______ 分钟.
(4)在整个上学的途中_________(哪个时间段)小明骑车速度最快,最快的速度是___________米/分.
查看答案和解析>>
科目:初中数学 来源: 题型:
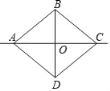
【题目】如图,四边形ABCD沿直线AC对折后重合,如果AC,BD交于O,AB∥CD,则结论①AB=CD,②AD∥BC,③AC⊥BD,④AO=CO,⑤AB⊥BC,其中正确的结论是___(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B是数轴上的两个点,它们分别表示的数是![]() 和1. 点A与点B之间的距离表示为AB.
和1. 点A与点B之间的距离表示为AB.
(1)AB= .
(2)点P是数轴上A点右侧的一个动点,它表示的数是![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
(3)点C为6. 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:![]() 的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
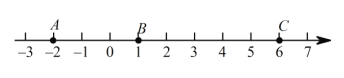
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABD中,AD=BD,点F是AD上的一个动点,过点A作AC⊥BF,交BF的延长线于点E,交BD的延长线于点C,则下列说法错误的是( )
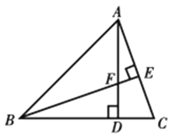
A.CD=DFB.AC=BFC.AD=BED.∠CAD+∠ABF=45°
查看答案和解析>>
科目:初中数学 来源: 题型:
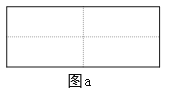
【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。

(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com