
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

【答案】(1)见解析;(2)∠BFC=100°
【解析】试题分析:(1)利用正方形的性质结合全等三角形的判定与性质得出△AFE≌△CFG进而得出AF=CF;
(2)利用正方形的对角线平分对角进而得出答案.
试题解析:(1)证明:∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,ED=GD,FE=FG.
∴AD-ED=CD-GD.
∴AE=CG.
在△AFE和△CFG中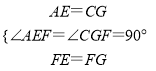 ,
,
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2)解:由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
连接DF,
∵四边形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°-∠CFG-∠GFD=180°-35°-45°=100°.
即∠BFC=100°.


科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
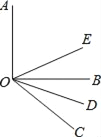
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
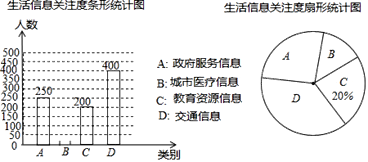
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( ) 
A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
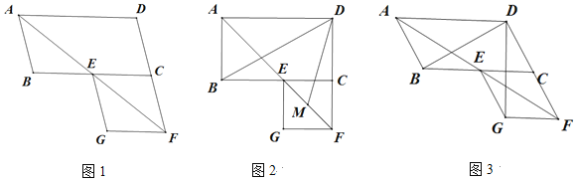
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:

(1)这32名学生培训前考分的中位数所在的等级是 ,培训后考分的中位数所在的等级是 .
(2)这32名学生经过培训,考分等级“不合格” 的百分比由 下降到 .
(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有 名.
(4)你认为上述估计合理吗:理由是什么?
答: ,理由: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com