
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
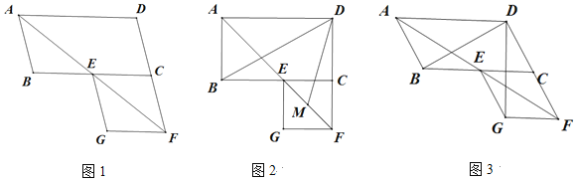
【答案】(1)证明见解析;
(2)∠BDM的度数为45°;
(3)∠BDG的度数为60°.
【解析】试题分析:(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形;
(2)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到∠BDM的度数;
(3)延长AB、FG交于H,连接HD,求证平行四边形AHFD为菱形,得出△ADH,△DHF为全等的等边三角形,证明△BHD≌△GFD,即可得出答案.
试题解析:(1)∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形.
(2)如图,连接BM,MC,
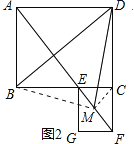
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵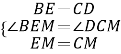
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形,
∴∠BDM=45°;
(3)∠BDG=60°,
延长AB、FG交于H,连接HD.
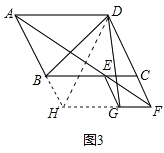
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形,
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=30°,∠ADC=120°,∠DFA=30°,
∴△DAF为等腰三角形,
∴AD=DF,
∴平行四边形AHFD为菱形,
∴△ADH,△DHF为全等的等边三角形,
∴DH=DF,∠BHD=∠GFD=60°,
∵FG=CE,CE=CF,CF=BH,
∴BH=GF,
在△BHD与△GFD中,
∵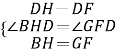 ,
,
∴△BHD≌△GFD(SAS),
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.


科目:初中数学 来源: 题型:
【题目】下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).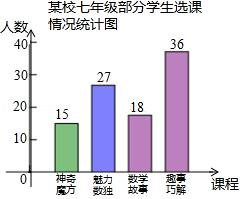
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图.根据该统计图,请估计该校七年级480名学生选“数学故事”的人数.
(2)学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
(AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中![]() ,
,![]() ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论:![]() ;
;![]() ;
;![]() ≌
≌![]() ;
;![]() 四边形ABCD的面积
四边形ABCD的面积![]() 其中正确的结论有
其中正确的结论有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com