
【题目】下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )

A.4个 B.3个 C.2个 D.1个
【答案】A
【解析】
试题分析:根据旋转、轴对称的定义来分析.
图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;
轴对称是指如果一个图形沿一条直线折叠,直线两侧的图形能够互相重合,就是轴对称.
解:图形1可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形2可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形3可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形4可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合.
故既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有4个.
故选A.


科目:初中数学 来源: 题型:
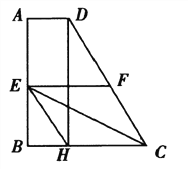
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有点a,b,c三点
![]()
(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
查看答案和解析>>
科目:初中数学 来源: 题型:
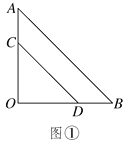
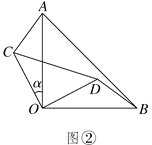
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
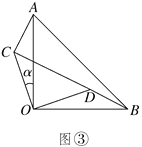
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
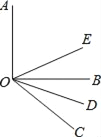
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
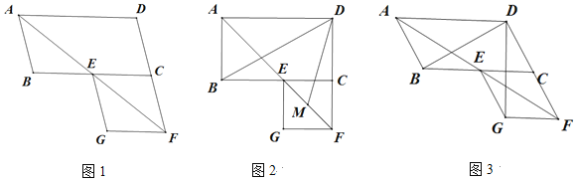
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com