
【题目】如图所示,I是△ABC三内角平分线的交点,IE⊥BC于E,AI延长线交BC于D,CI的延长线交AB于F,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.
(AB+BC﹣AC);④AC=AF+DC.其中正确的结论是_____.

【答案】①②③.
【解析】①∵I为△ABC三条角平分线的交点,IE⊥BC于E,
∴∠ABI=∠IBD,
∵∠DIC=∠DAC+∠ACI=![]() (∠BAC+∠ACB),∠ABI=
(∠BAC+∠ACB),∠ABI=![]() ∠ABC,
∠ABC,
∴∠CID+∠ABI=90°,
∵IE⊥BC于E,
∴∠BIE+∠IBE=90°,
∵∠ABI=∠IBE,
∴∠BIE=∠CID;
即①成立;
②∵I是△ABC三内角平分线的交点,
∴点I到△ABC三边的距离相等,
∴S△ABC=S△ABI+S△BCI+S△ACI=![]() ABIE+
ABIE+![]() BCIE+
BCIE+![]() ACIE=
ACIE=![]() IE(AB+BC+AC),
IE(AB+BC+AC),
即②成立;
③如图,过I作IH⊥AB于H,IG⊥AC于G,

∵I是△ABC三内角平分线的交点,
∴IE=IH=IG,
在Rt△AHI与Rt△AGI中,
![]() ,
,
∴Rt△AHT≌Rt△AGI(HL),
∴AH=AG,同理BE=BH,CE=CG,
∴BE+BH=AB+BC﹣AH﹣CE=AB+BC﹣AC,
∴BE=![]() (AB+BC﹣AC);
(AB+BC﹣AC);
即③成立;
④由③证得IH=IE,
∵∠FHI=∠IED=90°,
∴△IHF与△DEI不一定全等,
∴HF不一定等于DE,
∴AC=AG+CG=AH+CE≠AF+CD,
即④错误.
故答案为:①②③.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
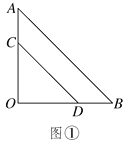
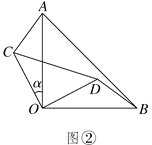
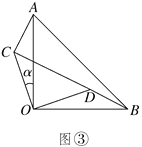
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
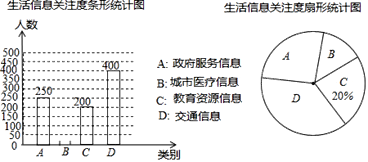
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
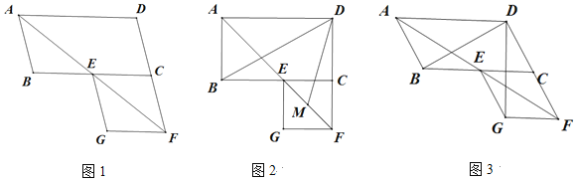
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程![]() 的解为
的解为![]() ,不等式组
,不等式组![]() 的解集为
的解集为![]() ,因为
,因为![]() ,所以,称方程
,所以,称方程![]() 为不等式组
为不等式组![]() 的关联方程.
的关联方程.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式组
中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程![]() ,
,![]() 都是关于
都是关于![]() 的不等式组
的不等式组![]() 的关联方程,求
的关联方程,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 ![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( ) 
A.π+1
B.π+2
C.2π+2
D.4π+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com