
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( ) 
A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2
【答案】B
【解析】解:∵AC与BD是⊙O的两条直径, ∴∠ABC=∠ADC=∠DAB=∠BCD=90°,
∴四边形ABCD是矩形,
∴△ABO于△CDO的面积=△AOD与△BOD 的面积,
∴图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD ,
∵OA=OB,
∴∠BAC=∠ABO=36°,
∴∠AOD=72°,
∴图中阴影部分的面积=2× ![]() =10π,
=10π,
故选B.
【考点精析】本题主要考查了圆周角定理和扇形面积计算公式的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.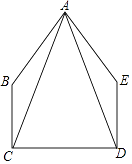
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.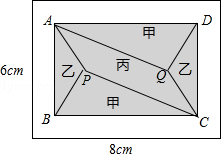
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD=CD,∠ABD=∠ACD=90°,点E、F分别在AB、AC上,若ED平分∠BEF.
(1)求证:FD平分∠EFC.
(2)若EF=4,AF=6,AE=5,求BE和CF的和的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】”切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时﹣﹣1.5小时;C:1.5小时﹣﹣2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图, 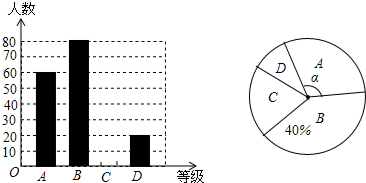
请根据图中信息解答下列问题:
(1)该校共调查了学生;
(2)请将条形统计图补充完整;
(3)表示等级A的扇形圆心角α的度数是;
(4)在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com