
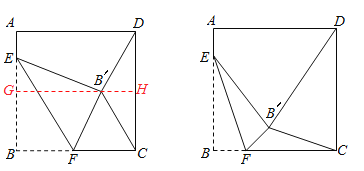
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 .

【答案】16或4![]() .
.
【解析】
试题(1)当B′D=B′C时,过B′点作GH∥AD,则∠B′GE=90°,当B′C=B′D时,AG=DH=![]() DC=8,由AE=3,AB=16,得BE=13.由翻折的性质,得B′E=BE=13,∴EG=AG﹣AE=8﹣3=5,∴B′G=
DC=8,由AE=3,AB=16,得BE=13.由翻折的性质,得B′E=BE=13,∴EG=AG﹣AE=8﹣3=5,∴B′G=![]() =
=![]() =12,∴B′H=GH﹣B′G=16﹣12=4,∴DB′=
=12,∴B′H=GH﹣B′G=16﹣12=4,∴DB′=![]() =
=![]() =
=![]() ;
;
(2)当DB′=CD时,则DB′=16(易知点F在BC上且不与点C、B重合);
(3)当CB′=CD时,∵EB=EB′,CB=CB′,∴点E、C在BB′的垂直平分线上,∴EC垂直平分BB′,由折叠可知点F与点C重合,不符合题意,舍去.
综上所述,DB′的长为16或![]() .故答案为:16或
.故答案为:16或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】数轴上从左到右有A,B,C三个点,点C对应的数是10,AB=BC=20.
(1)点A对应的数是 ,点B对应的数是 .
(2)动点P从A出发,以每秒4个单位长度的速度向终点C移动,同时,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,设移动时间为t秒.
①用含t的代数式表示点P对应的数是 ,点Q对应的数是 ;
②当点P和点Q间的距离为8个单位长度时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课![]() 分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数
分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为 理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数![]() 随时间
随时间![]() (分钟)的变化规律如图所示(其中
(分钟)的变化规律如图所示(其中![]() 都为线段)
都为线段)
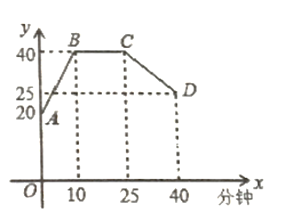
(1)分别求出线段![]() 和
和![]() 的函数解析式;
的函数解析式;
(2)开始上课后第![]() 分钟时与第
分钟时与第![]() 分钟时相比较,何时学生的注意力更集中?
分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲![]() 分钟,为了效果较好,要求学生的注意力指标数最低达到
分钟,为了效果较好,要求学生的注意力指标数最低达到![]() 那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )

A. BC=EC,∠B=∠E B. BC=EC,AC=DC
C. ∠B=∠E,∠A=∠D D. BC=EC,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0),B(0,2![]() )
)
(1)点(k+1,2k﹣5)关于x轴的对称点在第一象限,a为实数k的范围内的最大整数,求A点的坐标及△AOB的面积;
(2)在(1)的条件下如图1,点P是第一象限内的点,且△ABP是以AB为腰的等腰直角三角形,请直接写出P点坐标;
(3)在(1)的条件下,如图2,以AB、OB的作等边△ABC和等边△OBD,连接AD、OC交于E点,连接BE.
①求证:EB平分∠CED;
②M点是y轴上一动点,求AM+CM最小时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,一次函数的图像经过点
,一次函数的图像经过点![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() .
.

(1)求一次函数的表达式;
(2)二元一次方程组![]() 的解为________________;
的解为________________;
(3)当![]() 与
与![]() 同时成立时,
同时成立时,![]() 的取值范围为__________;
的取值范围为__________;
(4)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com