
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�A��a��0����B��0��2![]() ��
��
��1���㣨k+1��2k��5������x��ĶԳƵ��ڵ�һ���ޣ�aΪʵ��k�ķ�Χ�ڵ������������A������꼰��AOB�������
��2���ڣ�1������������ͼ1����P�ǵ�һ�����ڵĵ㣬�ҡ�ABP����ABΪ���ĵ���ֱ�������Σ���ֱ��д��P�����ꣻ
��3���ڣ�1���������£���ͼ2����AB��OB�����ȱߡ�ABC�͵ȱߡ�OBD������AD��OC����E�㣬����BE��
����֤��EBƽ�֡�CED��
��M����y����һ���㣬��AM+CM��Сʱ��M�����꣮

���𰸡���1��A��2��0����S��AOB��2![]() ����2��P������Ϊ��2+2
����2��P��������2+2![]() ��2����2
��2����2![]() ��2
��2![]() +2������3���������������M��0��
+2������3���������������M��0��![]() ����
����
��������
��1�����ݵ��ڵ��������ڣ��ó�����ʽ���������k�ķ�Χ�����������A���꣬����������������ʽ���ɵó����ۣ�
��2�����������������ȫ�����������PF��AF�����������P���ꣻ
��3�������жϳ���ABD�ա�CBO��SAS���������ó�S��ABD��S��CBO��AD��OC�����ɵó�BM��BN������ý�ƽ���ߵ��ж��������ɵó����ۣ�
�ڸ��ݺ�30�Ƚǵ�ֱ�������ε���������߶εij������������C���꣬���ֱ��A'C�Ľ���ʽ�����ɵó����ۣ�
�⣺��1���ߵ㣨k+1��2k��5������x��ĶԳƵ��ڵ�һ���ޣ�
��㣨k+1��2k��5���ڵ������ޣ�
��k+1��0��2k��5��0��
�ੁ1��k��2.5��
��aΪʵ��k�ķ�Χ�ڵ����������
��a��2��
��A��a��0����
��A��2��0����
��OA��2��
��B��0��2![]() ����
����
��OB��2![]() ��
��
��S��AOB��![]() OAOB��
OAOB��![]() ��
��![]() ��2
��2![]() ��
��
��2����ͼ1��
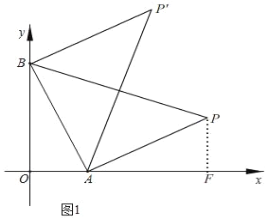
�ߵ�P�ǵ�һ�����ڵĵ㣬�ҡ�ABP����ABΪ���ĵ���ֱ�������Σ�
��ٵ���BAP��90��ʱ��AB��AP��
����P��PF��OA��F��
���PAF+��APF��90�㣬
�ߡ�BAP��90�㣬
���PAF+��BAO��90�㣬
���APF����BAO��
��AB��AP��
���OAB�ա�FPA��AAS����
��PF��OA��2��AF��OB��2![]() ��
��
��OF��OA+AF��2+2![]() ��
��
��P��2+2![]() ��2����
��2����
�ڵ���ABP��90��ʱ��ͬ�ٵķ����ã�P'��2![]() ��2
��2![]() +2����
+2����
����P��������2+2![]() ��2����2
��2����2![]() ��2
��2![]() +2����
+2����
��3������ͼ2��
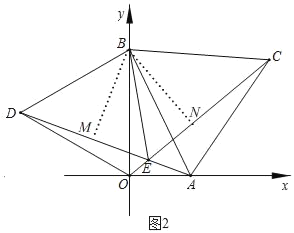
�ߡ�OBD�͡�ABC���ǵȱ������Σ�
��BD��OB��AB��BC����OBD����ABC��60�㣬
���ABD����CBO��
�ڡ�ABD�͡�CBO�У� ��
��
���ABD�ա�CBO��SAS����
��S��ABD��S��CBO��AD��OC��
����B��BM��AD��M��BN��OC��N��
��BM��BN��
��BM��AD��BN��OC��
��BE�ǡ�CED�Ľ�ƽ���ߣ�
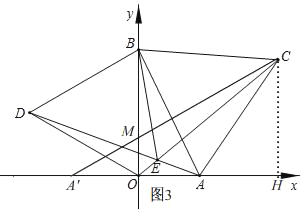
����ͼ3��
����A����y��ĶԳƵ�A'��
��A��2��0����
��A'����2��0����
����A'C��y����M��
����C��CH��OA��H��
��Rt��AOB��OA��2��OB��2![]() ��
��
��AB��4��tan��OAB��![]() ��
��![]() ��
��![]() ��
��
���OAB��60�㣬
�ߡ�ABC�ǵȱ������Σ�
��AC��AB��4����BAC��60�㣬
���CAH��60�㣬
��Rt��ACH�У���ACH��90�㩁��CAH��30�㣬
��AH��2��CH��2![]() ��
��
��OH��OA+AH��4��
���C��4��2![]() ����
����
��A'����2��0����
��ֱ��A'C�Ľ���ʽΪy��![]() x+
x+![]() ��
��
��M��0��![]() ����
����


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD=BC=12��AB=CD��BD=15����E��D���������ÿ��4����λ���ٶ���D��A��D�����ƶ�����F�ӵ�C��������ÿ��1����λ���ٶ���CB���B�������ƶ�����G�ӵ�B������BD���D�����ƶ���������ͬʱ����������һ���㵽���յ�ʱ����������Ҳ��ֹ֮ͣ�˶��������ƶ�ʱ��Ϊt�룮

��1����˵����AD��BC��
��2�����ƶ������У�С����������DEG����BFGȫ�ȵ�������֣�����̽���������������ּ��Σ����ֱ������ʱ���ƶ�ʱ��t��G����ƶ����룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳���16����E�ڱ�AB�ϣ�AE=3����F�DZ�BC�ϲ����B��C�غϵ�һ�����㣬����EBF��EF�۵�����B����B����������CDB��ǡΪ���������Σ���DB���ij�Ϊ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ֱ�Ĺ�·����![]() ��
��![]() ���أ���������ͬʱ�������������г���
���أ���������ͬʱ�������������г���![]() �ص�
�ص�![]() �أ��������г���
�أ��������г���![]() �ص�
�ص�![]() �أ�����
�أ�����![]() �غ�������ԭ·����
�غ�������ԭ·����![]() ��.��ͼ�Ǽס���������
��.��ͼ�Ǽס���������![]() �صľ���
�صľ���![]() ����ʻʱ��
����ʻʱ��![]() ֮��ĺ���ͼ������˵���Т�
֮��ĺ���ͼ������˵���Т�![]() ��
��![]() �������30ǧ�ף��ڼ��ٶ�Ϊ15ǧ��/ʱ���۵�
�������30ǧ�ף��ڼ��ٶ�Ϊ15ǧ��/ʱ���۵�![]() ������Ϊ(
������Ϊ(![]() ��20)���ܵ��ס����������10ǧ��ʱ�����ǵ���ʻʱ����
��20)���ܵ��ס����������10ǧ��ʱ�����ǵ���ʻʱ����![]() Сʱ��
Сʱ��![]() Сʱ. ��ȷ�ĸ���Ϊ( )
Сʱ. ��ȷ�ĸ���Ϊ( )

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ͬһƽֱ��·��A��������ʻ����;��ͣ������ǰ���յ�B�أ��ס�������֮��ľ���S��ǧ�ף���׳���ʻ��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ������˵����
�ټס����������210ǧ�ף��ڼ��ٶ�Ϊ60ǧ��/Сʱ�������ٶ�Ϊ120ǧ��/Сʱ�����ҳ�����ʻ3 ![]() Сʱ��������ȷ�ĸ���Ϊ�� ��
Сʱ��������ȷ�ĸ���Ϊ�� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͳ�������Ǽ�3�·�ÿ�δ�绰��ͨ��ʱ��������ͳ�ƽ�����з���(ÿ�麬��Сֵ���������ֵ) ,�������Ľ�����Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ��������˵���в���ȷ���ǣ� ��
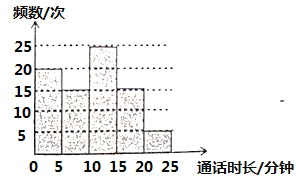
A.������3�·ݴ�绰����Ƶ��Ϊ![]() ��
��
B.������3�·�ÿ�δ�绰��ͨ��ʱ����![]() �����Ƶ��Ϊ
�����Ƶ��Ϊ![]() ��
��
C.������3�·�ÿ�δ�绰��ͨ��ʱ����![]() �����Ƶ�����
�����Ƶ�����
D.������3�·�ÿ�δ�绰��ͨ��ʱ����![]() �����Ƶ��Ϊ
�����Ƶ��Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������գ�
(1)1,3,5,7,9��__________��
(2)2,5,8,11,14��__________��
(3)![]() ��
��![]() ��
��![]() ��
��![]() ��__________��
��__________��
(4)![]() ��
��![]() ��
��![]() ��
��![]() ��__________��
��__________��
(5)2,6,15,31,56��__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A1��A2��A3������An��������y=x2ͼ���ϣ���B1��B2��B3������Bn��y���ϣ�����A1B0B1����A2B1B2��������AnBn��1Bn��Ϊ����ֱ�������Σ���B0������ԭ�㣩�����A2014B2013B2014���������ڣ� ��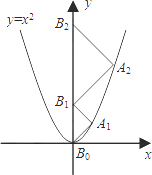
A.2013
B.2014
C.2013 ![]()
D.2014 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У���x��0ʱ��y��ֵ��x��ֵ�����������ǣ� ��
A.y=��x2
B.y=x��1
C.y=��x+1
D.y= ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com