
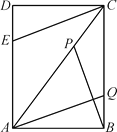
【题目】如图,矩形ABCD中,∠ABC=90,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).
(1)若△CDE与△ADC相似,求t的值.
(2)连接AQ,BP,CE,若BP⊥CE,求t的值;
(3)当PQ长度取得最小值时,求t的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由题意可得CD2=DEDA,即36=4t×8,解方程即可.
(2)如图1中,作PM⊥BC于M.由△PMB∽△QBA,得![]() ,由CP=5t,CM=4t,PM=3t,可得方程
,由CP=5t,CM=4t,PM=3t,可得方程![]() ,解方程即可.
,解方程即可.
(3)根据PQ=![]() ,利用二次函数的性质即可解决问题.
,利用二次函数的性质即可解决问题.
试题解析:(1)∵0<t<2,
∴点E与点A不重合,
∵△CDE与△ADC相似,
∴∠DCE=∠DAC,
∴![]() ,
,
CD2=DEDA,即36=4t×8,
解得t=![]() s.
s.
(2)如图1,

∵DE=BQ=4t,AD=BC,AD∥BC
∴AE=CQ,AE∥CQ,
∴四边形AECQ为平行四边形,
∴CE∥AQ,过点P做PM⊥CB于点M,
∵BP⊥CE,CE∥AQ,
∴BP⊥AQ,
∴∠ABP+∠PBM=90°,∠BAQ+∠PBA=90°,
∴∠BAQ=∠PBM,∵∠ABQ=∠PMB=90°.
∴△PMB∽△QBA,
∴![]() ,
,
∵CP=5t,CM=4t,PM=3t,
∴![]() ,
,
所以t=![]() s.
s.
(3)如图2,
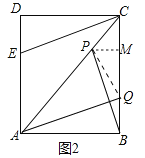
在Rt△PMQ中,PQ=![]() ,
,
所以当t=-![]() s时,PQ可以取得最小值.
s时,PQ可以取得最小值.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
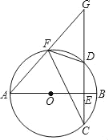
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是弧AD上的一点,AF,CD的延长线相交于点G.
(1)若⊙O的半径为3![]() ,且∠DFC=45°,求弦CD的长.
,且∠DFC=45°,求弦CD的长.
(2)求证:∠AFC=∠DFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织七年级800名学生参加诗词大赛,为了解学生整体的诗词积累情况,随机抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的列图表,解答问题:
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 40 | 0.20 |
三 | 70.5~80.5 | 50 | 0.25 |
四 | 80.5~90.5 | m | 0.35 |
五 | 90.5~100.5 | 24 | n |
(1)本次抽样中,表中m=____,n=____,样本成绩的中位数落在第____组内.
(2)补全频数分布直方图.
(3)若规定成绩超过80分为优秀,请估计该校七年级学生中诗词积累成绩为优秀的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
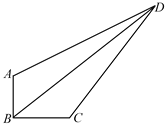
【题目】如图,在四边形ABCD中,∠ABC=90,AB=3,BC=4,CD=10,DA=![]() ,则四边形ABCD的面积为=____________,BD的长为____________.
,则四边形ABCD的面积为=____________,BD的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
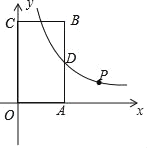
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.

已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,点B的坐标为(4,m)(5≤m≤7),反比例函数y=![]() (x>0)的图象交边AB于点D.
(x>0)的图象交边AB于点D.
(1)用m的代数式表示BD的长;
(2)设点P在该函数图象上,且它的横坐标为m,连结PB,PD
①记矩形OABC面积与△PBD面积之差为S,求当m为何值时,S取到最大值;
②将点D绕点P逆时针旋转90°得到点E,当点E恰好落在x轴上时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
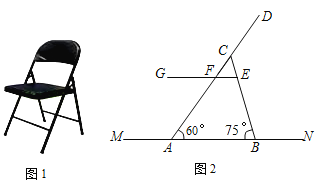
【题目】如图1是一把折叠椅子,如图2是椅子完全打开支稳后的侧面示意图,![]() 表示地面所在的直线,其中
表示地面所在的直线,其中![]() 和
和![]() 表示两根较粗的钢管,
表示两根较粗的钢管,![]() 表示座板平面,
表示座板平面,![]() ,交
,交![]() 于点F,且
于点F,且![]() ,
,![]() 长
长![]() ,
,![]() ,
,![]() 长24cm,
长24cm,![]() 长24cm,
长24cm,
(1)求座板![]() 的长;
的长;
(2)求此时椅子的最大高度(即点D到直线![]() 的距离).(结果保留根号)
的距离).(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:
请解答下列问题:
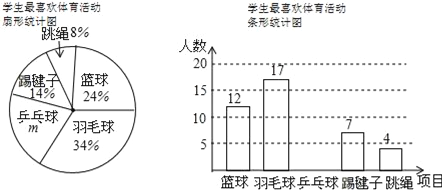
(1)m= %,这次共抽取了 名学生进行调查;请补全条形统计图;
(2)若全校有800名学生,则该校约有多少名学生喜爱打篮球?
(3)学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com