
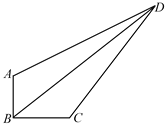
【题目】如图,在四边形ABCD中,∠ABC=90,AB=3,BC=4,CD=10,DA=![]() ,则四边形ABCD的面积为=____________,BD的长为____________.
,则四边形ABCD的面积为=____________,BD的长为____________.
【答案】31; ![]()
【解析】
试题解析:连接AC,过点D作DE⊥BC,交BC的延长线与点E.

因为∠ABC=90°,AB=3,BC=4,
∴AC=![]() =5,
=5,
由于AC2+CD2=25+100=125,AD2=(5![]() )2=125,
)2=125,
∴AC2+CD2=AD2.
所以∠ACD=90°.
所以S四边形ABCD=S△ABD+S△ACD
=![]() ABBC+
ABBC+![]() ACCD
ACCD
=![]() ×3×4+
×3×4+![]() ×5×10
×5×10
=6+25=31.
∵∠DEC=90°,∴∠DCE+∠CDE=90°,
所以∠DCE+∠ACB=90°,
∴∠CDE=∠ACB,又∵∠ABC=90°,
∴△ABC∽△CED
![]()
∴CE=6,DE=8.
∴BE=BC+CE=10,
在Rt△DEB中,
DB=![]() .
.


科目:初中数学 来源: 题型:
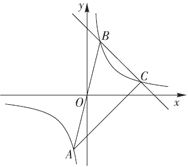
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 与点
与点![]() 关于原点对称,一次函数
关于原点对称,一次函数![]() 的图象经过点
的图象经过点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
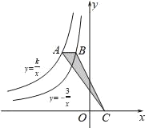
【题目】如图,点A是反比例函数y=![]() 图象上一点,过点A作x轴的平行线交反比例函数y=﹣
图象上一点,过点A作x轴的平行线交反比例函数y=﹣![]() 的图象于点B,点C在x轴上,且S△ABC=
的图象于点B,点C在x轴上,且S△ABC=![]() ,则k=( )
,则k=( )
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
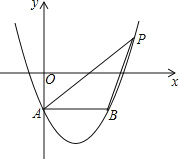
【题目】如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
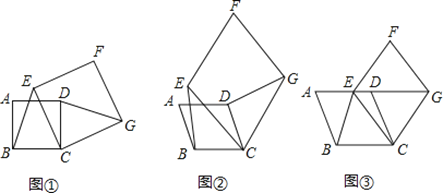
【题目】感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.
探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
应用:如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED, ∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
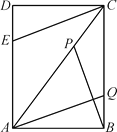
【题目】如图,矩形ABCD中,∠ABC=90,AB=6cm,BC=8cm,动点P从点C出发,在线段AC上以每秒5cm的速度向点A匀速运动,同时动点Q从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,动点E从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2).
(1)若△CDE与△ADC相似,求t的值.
(2)连接AQ,BP,CE,若BP⊥CE,求t的值;
(3)当PQ长度取得最小值时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)图象上,点B在反比例函数y=
(x>0)图象上,点B在反比例函数y=![]() (k>0,x>0)的图象上,AB∥x轴,BC∥y轴交x轴于点C,连结AC,交反比例函数y=
(k>0,x>0)的图象上,AB∥x轴,BC∥y轴交x轴于点C,连结AC,交反比例函数y=![]() (x>0)图象于点D,若D为AC的中点,则k的值是( )
(x>0)图象于点D,若D为AC的中点,则k的值是( )

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离公式为:d=![]() ,
,
例如,求点P(1,3)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知:A=4,B=3,C=﹣3
所以P(1,3)到直线4x+3y﹣3=0的距离为:d=![]() =2
=2
根据以上材料,解决下列问题:
(1)求点P1(1,-1)到直线3x﹣4y﹣5=0的距离.
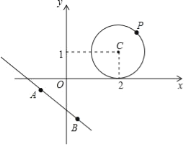
(2)已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
(3)如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出△ABP面积的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com