解:∵点M的速度为1cm/s,点N的速度为2cm/s,
∴若点M运动到点D,则t=15÷1=15秒,
过点N运动到点B,则t=21÷2=10.5秒,
∵一点到达端点时,另一点也随之停止运动,
∴0<t≤10.5,
(1)∵点M的速度为1cm/s,点N的速度为2cm/s,
∴MD=AD-AM=15-t,CN=2t,
四边形MNCD是平行四边形时,MD=CN,
∴15-t=2t,
解得t=5;
(2)∵点M的速度为1cm/s,点N的速度为2cm/s,
∴AM=t,BN=BC-CN=21-2t,
四边形MNCD是直角梯形时,AM=BN,
∴t=21-2t,
解得t=7;
(3)如图,过点D作DE⊥BC于E,
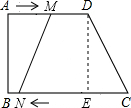
∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=15cm,
∴CE=BC-BE=21-15=6cm,
四边形MNCD是等腰梯形时,CN=2CE+MD,
∴2t=2×6+15-t,
解得t=9.
分析:先求出t的取值范围.
(1)用t表示出MD、CN,然后根据平行四边形对边相等可得MD=CN,然后计算即可得解;
(2)用t表示出AM、BN,然后根据四边形MNCD是直角梯形时,AM=BN,列出方程计算即可得解;
(3)过点D作DE⊥BC于E,然后判断出四边形ABED是矩形,根据矩形的对边相等求出BE,再求出CE,然后表示出MD,再根据等腰梯形的性质,四边形MNCD为等腰梯形时,CN=2CE+MD,列出方程求解即可.
点评:本题考查了梯形,平行四边形的性质,直角梯形的性质,等腰梯形的性质,熟练掌握各图形的性质,分别列出关于t的方程是解题的关键.

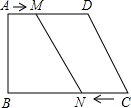 停止运动,设运动时间为t秒.
停止运动,设运动时间为t秒.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )