Question

【题目】如图所示，已知O为坐标原点，长方形ABCD（点A与坐标原点重合）的顶点D、B分别在x轴、y轴上，且点C的坐标为（-4，8），连接BD，将△ABD沿直线BD翻折至△ABD，交CD于点E．

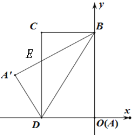
（1）求S△BED的面积；

（2）求点A坐标.

Answer 1

【答案】（1）10；（2）A’（－，）

【解析】

（1）根据矩形的性质以及翻折的性质得出DE=BE，再在Rt△BCE中利用勾股定理即可得出CE=3,DE=BE=5，从而可以求出答案；

（2）过点A’作A‘OB于N，交CD于M，易证△A’ED≌△CEB，，利用面积可得出A’E，在Rt△A’DF中，由勾股定理可得DF，从而得出答案。

解：（1）得BC=4，CD=8，易证△BED是等腰三角形，则BE=DE，设DE＝x,∴BE=x，CE=8-x,

在Rt△CBE中，由勾股定理得x2=42+（8-x）2 ∴x=5

∴S△BED=10

（2）过点A’作A‘OB于N，交CD于M，

∵∠C=∠A’,∠CEB=∠A’ED,DE=BE

∴△A’ED≌△CEB，

则A’E=3, A’D=4,DE=5

∴A’M=,∴A’N=A’M+M’N=

∴在Rt△A’MD中，MD==

又A’在第二象限，则A’（ －，）