
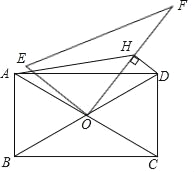
【题目】如图,在矩形ABCD中,AB=4,BC=4![]() ,对角线AC、BD相交于点O,现将一个直角三角板OEF的直角顶点与O重合,再绕着O点转动三角板,并过点D作DH⊥OF于点H,连接AH.在转动的过程中,AH的最小值为_____.
,对角线AC、BD相交于点O,现将一个直角三角板OEF的直角顶点与O重合,再绕着O点转动三角板,并过点D作DH⊥OF于点H,连接AH.在转动的过程中,AH的最小值为_____.
【答案】2![]() ﹣2
﹣2
【解析】
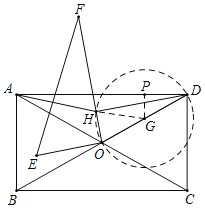
取OD的中点G,过G作GP⊥AD于P,连接HG,AG,依据∠ADB=30°,可得PG![]() DG=1,依据∠DHO=90°,可得点H在以OD为直径的⊙G上,再根据AH+HG≥AG,即可得到当点A,H,G三点共线,且点H在线段AG上时,AH最短,根据勾股定理求得AG的长,即可得出AH的最小值.
DG=1,依据∠DHO=90°,可得点H在以OD为直径的⊙G上,再根据AH+HG≥AG,即可得到当点A,H,G三点共线,且点H在线段AG上时,AH最短,根据勾股定理求得AG的长,即可得出AH的最小值.
如图,取OD的中点G,过G作GP⊥AD于P,连接HG,AG.
∵AB=4,BC=4![]() AD,∴BD
AD,∴BD![]() 8,∴BD=2AB,DO=4,HG=2,∴∠ADB=30°,∴PG
8,∴BD=2AB,DO=4,HG=2,∴∠ADB=30°,∴PG![]() DG=1,∴PD
DG=1,∴PD![]() ,AP=3
,AP=3![]() .
.
∵DH⊥OF,∴∠DHO=90°,∴点H在以OD为直径的⊙G上.
∵AH+HG≥AG,∴当点A,H,G三点共线,且点H在线段AG上时,AH最短,此时,Rt△APG中,AG![]() ,∴AH=AG﹣HG=2
,∴AH=AG﹣HG=2![]() 2,即AH的最小值为2
2,即AH的最小值为2![]() 2.
2.
故答案为:2![]() 2.
2.


科目:初中数学 来源: 题型:
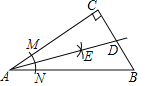
【题目】如图,在Rt△ABC中,∠C=90°,以原点A为圆心,适当的长为半径画弧,分别交AC,AB于点M,N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点E,作射线AE交BC于点D,若BD=5,AB=15,△ABD的面积30,则AC+CD的值是( )
MN的长为半径画弧,两弧交于点E,作射线AE交BC于点D,若BD=5,AB=15,△ABD的面积30,则AC+CD的值是( )
A. 16B. 14C. 12D. 5![]() +4
+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把![]() 的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:![]() .如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=
.如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=![]() ,则S△A′E′F′=__
,则S△A′E′F′=__

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P,Q在数轴上分别表示的数分别为p,q,我们把p,q之差的绝对值叫做点P,Q之间的距离,即![]() .如图,在数轴上,点A,B,O,C,D的位置如图所示,则
.如图,在数轴上,点A,B,O,C,D的位置如图所示,则![]() ;
;![]() ;
;![]() .请探索下列问题:
.请探索下列问题:
![]()
(1)计算![]() ____________,它表示哪两个点之间的距离?________________________.
____________,它表示哪两个点之间的距离?________________________.
(2)点M为数轴上一点,它所表示的数为x,用含x的式子表示PB=____________;当PB=2时,x=____________;当x=____________时,|x+4|+|x-1|+|x-3|的值最小.
(3)|x-1|+|x-2|+|x-3|+…+|x-2018|+|x-2019|的最小值为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
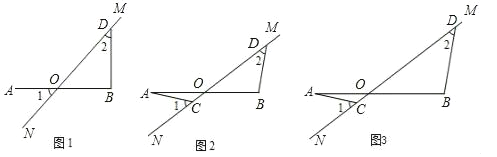
【题目】在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.
(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
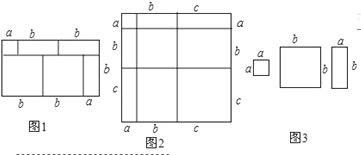
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
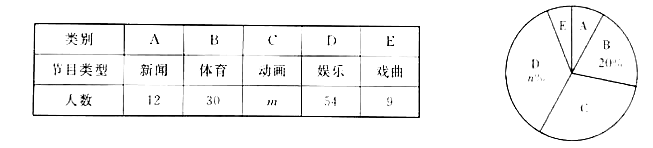
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中![]() 的值为 ,统计图中
的值为 ,统计图中![]() 的值为 ;
的值为 ;
(3)在统计图中,![]() 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com