Question

已知四个互不相等的实数x₁，x₂，x₃，x₄，其中x₁＜x₂，x₃＜x₄．
（1）请列举x₁，x₂，x₃，x₄从小到大排列的所有可能情况；
（2）已知a为实数，函数y=x²-4x+a与x轴交于（x₁，0），（x₂，0）两点，函数y=x²+ax-4与x轴交于（x₃，0），（x₄，0）两点．若这四个交点从左到右依次标为A，B，C，D，且AB=BC=CD，求a的值．

Answer 1

【答案】分析：（1）可以这样理解：x₁或x₃最小，x₂或x₄最大，以此排列即可；
（2）将利用二次函数两点间的距离公式解答．
解答：解：（1）x₁＜x₂＜x₃＜x₄，x₁＜x₃＜x₂＜x₄，x₁＜x₃＜x₄＜x₂，x₃＜x₄＜x₁＜x₂，x₃＜x₁＜x₄＜x₂，x₃＜x₁＜x₂＜x₄；

（2）上述6种情况中第3，6种情况不可能出现．否则，两个函数的对称轴相同，则a=-4，从而x₁=x₃，x₂=x₄，这与题意不符，
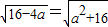
在其他4种情况中，都有|x₂-x₁|=|x₄-x₃|，因此有，即a=0或-4（舍去），经检验a=0满足题意．
点评：解答此题要明确两点间的距离公式：|x₂-x₁|=．
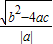