
【题目】下表是某班同学随机投掷一枚硬币的试验结果( )
抛掷次数n | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数m | 22 | 52 | 71 | 95 | 116 | 138 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.47 | 0.48 | 0.46 | 0.46 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的概率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是( )
A. ①②B. ①③C. ③D. ②③
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。
查看答案和解析>>
科目:初中数学 来源: 题型:
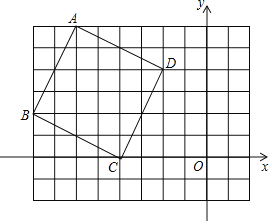
【题目】如图,在平面直角坐标系中,四边形ABCD的坐标分别为A(﹣6,6),B(﹣8,2),C(﹣4,0),D(﹣2,4).
(1)画出一个四边形A′B′C′D′,使四边形A′B′C′D′与四边形ABCD是以原点O为位似中心,相似比为1:2的位似图形.
(2)直接写出点的坐标:A′( ),B′( ),C′( ),D′( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() ,
,![]() .若动点
.若动点![]() 从
从![]() 开始沿
开始沿![]() 向
向![]() 以每秒1个单位长度的速度运动,同时动点
以每秒1个单位长度的速度运动,同时动点![]() 从
从![]() 开始沿
开始沿![]() 向
向![]() 以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为
以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为![]() 秒.
秒.
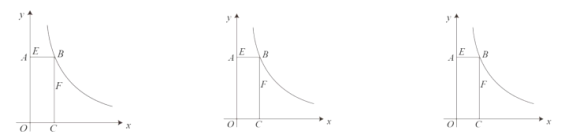
(1)求反比例函数的表达式;
(2)当![]() 时,在
时,在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 的周长最小,请求出此时点
的周长最小,请求出此时点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的周长最小值;
的周长最小值;
(3)在双曲线上是否存在一点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出满足条件
为顶点的四边形是平行四边形?若存在,请直接写出满足条件![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,AD=8,O为AD中点,P是线段AO上一动点,以O为圆心,OP为半径作⊙O分别交BO及BO延长线于点E,F,延长AE交BC于点H.
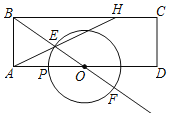
(1)当OP=2时,求BH的长.
(2)当AH交⊙O于另一点G时,连接FG,DF,作DM⊥BF于点M,求证:△EFG∽△FDM.
(3)连结HO,当△EHO是直角三角形时,求OP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com