
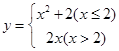 ,则当函数值
,则当函数值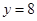 时,自变量
时,自变量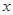 的值是( )
的值是( )A.± | B.4 | C.± 或4 或4 | D.4或- |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:单选题
 ,当自变量
,当自变量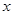 取
取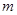 时,对应的函数值大于0,当自变量
时,对应的函数值大于0,当自变量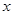 分别取
分别取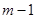 ,
,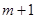 时对应的函数值
时对应的函数值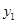 、
、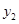 ,则
,则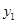 ,
,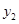 满足
满足 A.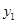 >0, >0,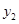 >0 >0 | B.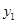 <0, <0,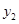 <0 <0 | C.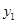 <0, <0,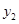 >0 >0 | D.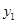 >0, >0,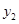 <0 <0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 过点A(0,4)和C(8,0),P(t,0)是
过点A(0,4)和C(8,0),P(t,0)是 轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过B作
轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过B作 轴的垂线、过点A作
轴的垂线、过点A作 轴的垂线,两直线相交于点D.
轴的垂线,两直线相交于点D.

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
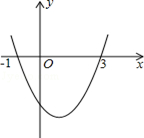
| A.3个 | B.2个 | C.1个 | D.0个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
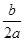 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值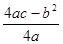
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
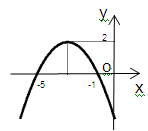
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
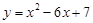 的最大值.他画图研究后发现,
的最大值.他画图研究后发现,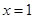 和
和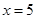 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对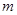 进行分类讨论.
进行分类讨论.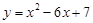 的对称轴为直线
的对称轴为直线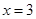 ,
,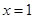 和
和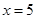 时的函数值相等.
时的函数值相等.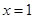 时,
时,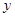 的最大值为2;
的最大值为2;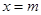 时,
时,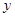 的最大值为
的最大值为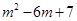 .
.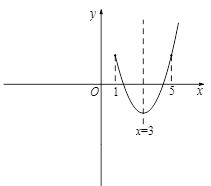
 ≤x≤4时,二次函数
≤x≤4时,二次函数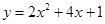 的最大值为_______;
的最大值为_______;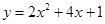 的最大值;
的最大值;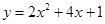 的最大值为31,则
的最大值为31,则 的值为_______.
的值为_______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com