
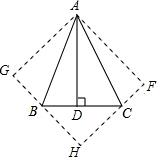
 如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.分析 (1)由折叠的性质可得到的条件是:①AG=AD=AF,②∠GAF=∠GAD+∠DAF=2∠BAC=90°,且∠G=∠F=90°;由②可判定四边形AGHF是矩形,由AG=AF可证得四边形AGHF是正方形;
(2)设AD=x,由折叠的性质可得:AD=AF=x(即正方形的边长为x),BG=BD=6,CF=CD=4;进而可用x表示出BH、HC的长,即可在Rt△BHC中,由勾股定理求得AD的长,进而可求出AB的长.
解答 证明:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°;
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°;
∴∠GAF=∠BAG+∠CAF+∠BAC=90°;
∴四边形AFHG是正方形,
解:(2)∵四边形AFHG是正方形,
∴∠BHC=90°,
又GH=HF=AD,GB=BD=6,CF=CD=4;
设AD的长为x,则BH=GH-GB=x-6,CH=HF-CF=x-4.
在Rt△BCH中,BH2+CH2=BC2,
∴(x-6)2+(x-4)2=102,
解得x1=12,x2=-2(不合题意,舍去),
∴AD=12,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{144+36}$=6$\sqrt{5}$.
点评 此题主要考查了垂径定理、勾股定理、正方形的判定和性质以及图形的翻折变换等知识,能够根据折叠的性质得到与所求相关的相等角和相等边是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.
如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
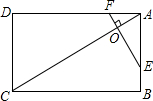 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
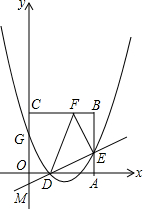 如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.
如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
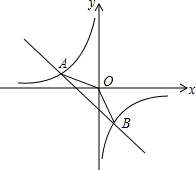 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 562.5元 | B. | 875元 | C. | 550元 | D. | 750元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com