
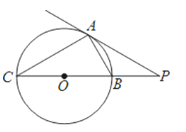
【题目】如图,点P是⊙O外一点,过点P作⊙O的切线,切点为A,连接PO并延长,交⊙O于B、C两点.
(1)求证:△PBA∽△PAC;
(2)若∠BAP=30°,PB=2,求⊙O的半径.
【答案】(1)证明见解析(2)2
【解析】
(1)利用弦切角定理可以证明:∠PAB=∠C,则△PBA和△PAC中有两个角对应相等,则一定相似;
(2)易证△OAB是等边三角形,再证明AB=BP,即可求解.
(1)证明:∵PA作⊙O的切线,切点为A,
∴∠PAB=∠C,
又∵∠P=∠P,
∴△PBA∽△PAC;
(2)∵PA作⊙O的切线,切点为A,
∴∠OAP=90°,
∵∠BAP=30°,
∴∠OAB=60°,
∵OA=OB,
∴∠ABO=60°,
∴∠P=30°
∴∠AOB=90°﹣∠P=90°﹣30°=60°.
∵OA=OB
∴△OAB是等边三角形.
∴OB=AB.
∵PA作⊙O的切线,切点为A,
∴∠PAB=![]() ∠AOB=30°,
∠AOB=30°,
∴∠PAB=∠P,
∴AB=BP
∴OB=AB=BP=2.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
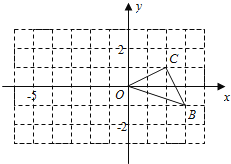
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便广大游客到昆明参观游览,铁道部门临时增开了一列南宁——昆明的直达快车,已知南宁、昆明两站的路程为828千米,一列普通快车与一列直达快车都由南宁开往昆明,直达快车的平均速度是普通快车平均速度的1.5倍,直达快车比普通快车后出发2小时,而先于普通快车4小时到达昆明,分别求出两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
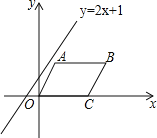
【题目】如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过______秒该直线可将平行四边形OABC分成面积相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,点D为BC中点.∠MDN=900,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论
①(BE+CF)=![]() BC,②
BC,②![]() ,③
,③![]() AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
AD·EF,④AD≥EF,⑤AD与EF可能互相平分,
其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
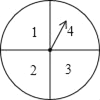
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
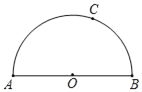
【题目】如图,AB为半圆O的直径,点C为半圆上任一点.
(1)若∠BAC=30°,过点C作半圆O的切线交直线AB于点P.求证:△PBC≌△AOC;
(2)若AB=6,过点C作AB的平行线交半圆O于点D.当以点A,O,C,D为顶点的四边形为菱形时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com