分析:(1)由于原式中含有括号,则先去括号,在去括号时应先去小括号然后去中括号,去完括号再进行合并同类项.
(2)由于原式中含有幂运算,则先做幂运算,然后去括号和绝对值符号,在做运算时应先做乘除运算,再做加减.
(3)先对等式左边化简,在化简时先去括号,然后合并同类项,最后解方程得到x的值.
(4)由于整式中含有分式,则先通过通分将分式化为整式.然后解方程.
解答:解:(1)6xy-3[3y
2-(x
2-2xy)+1],
=6xy-3[3y
2-x
2+2xy+1],
=6xy-9y
2+3x
2-6xy-3,
=3x
2-9y
2-3;
(2)-1
4÷(-5)
2×(-
)+|0.8-1|,
=-1÷25×(-
)+|0.8-1|,
=
+0.2,
=
;
(3)等式左边=x-2(x-3x+3)=x-2x+6x-6=5x-6,
∴方程可化为5x-6=8,
移项并合并,得
5x=14,
系数化为1得
x=2.8;
(4)去分母,得
2(x+1)-(x-2)=3(4-x)+6,
去括号得:
2x+2-x+2=12-3x+6,
移项,得
2x-x+3x=12+6-2-2,
合并同类项,得
4x=14,
系数化为1,得
x=3.5.
点评:本题主要考查整式的混合运算和一元一次不等式的解法,需要熟练掌握.



 名校课堂系列答案
名校课堂系列答案 )+|0.8﹣1|
)+|0.8﹣1|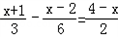 +1.
+1.