关于x的一元二次方程x2-(m-3)x-m2=0.
(1)证明:方程总有两个不相等的实数根;
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|-2,求m的值及方程的根.
【答案】
分析:(1)找出一元二次方程中的a,b及c,表示出b
2-4ac,然后判断出b
2-4ac大于0,即可得到原方程有两个不相等的实数根;
(2)利用根与系数的关系表示出两根之和与两根之积,判断出两根之积小于0,得到两根异号,分两种情况考虑:若x
1>0,x
2<0,利用绝对值的代数意义化简已知的等式,将表示出的两根之和代入,列出关于m的方程,求出方程的解得到m的值,进而确定出方程,求出方程的解即可;若x
1<0,x
2>0,同理求出m的值及方程的解.
解答:解:(1)一元二次方程x
2-(m-3)x-m
2=0,
∵a=1,b=-(m-3)=3-m,c=-m
2,
∴△=b
2-4ac=(3-m)
2-4×1×(-m
2)=5m
2-6m+9=5(m-

)
2+
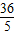
,
∴△>0,
则方程有两个不相等的实数根;
(2)∵x
1•x
2=
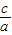
=-m
2≤0,x
1+x
2=m-3,
∴x
1,x
2异号,
又|x
1|=|x
2|-2,即|x
1|-|x
2|=-2,
若x
1>0,x
2<0,上式化简得:x
1+x
2=-2,
∴m-3=-2,即m=1,
方程化为x
2+2x-1=0,
解得:x
1=-1+
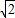
,x
2=-1-
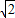
,
若x
1<0,x
2>0,上式化简得:-(x
1+x
2)=-2,
∴x
1+x
2=m-3=2,即m=5,
方程化为x
2-2x-25=0,
解得:x
1=1-
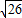
,x
2=1+
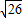
.
点评:此题考查了一元二次方程根的判别式,以及根与系数的关系,一元二次方程ax
2+bx+c=0(a≠0),当b
2-4ac>0时,方程有两个不相等的实数根;当b
2-4ac=0时,方程有两个相等的实数根;当b
2-4ac<0时,方程没有实数根.

 )2+
)2+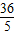 ,
,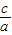 =-m2≤0,x1+x2=m-3,
=-m2≤0,x1+x2=m-3,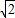 ,x2=-1-
,x2=-1-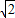 ,
,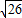 ,x2=1+
,x2=1+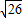 .
.
