练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

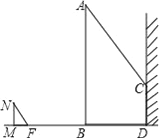
    【题目】如图，一电线杆AB的影子分别落在了地上和墙上．同一时刻，小明竖起1米高的直杆MN，量得其影长MF为0.5米，量得电线杆AB落在地上的影子BD长3米，落在墙上的影子CD的高为2米．你能利用小明测量的数据算出电线杆AB的高吗？

    【答案】电线杆AB的高为8米

    【解析】试题分析：过C点作CG⊥AB于点G，把直角梯形ABCD分割成一个直角三角形和一个矩形，由于太阳光线是平行的，就可以构造出相似三角形，根据相似三角形的性质解答即可．

    试题解析：过C点作CG⊥AB于点G，∴GC＝BD＝3米，GB＝CD＝2米，∵∠NMF＝∠AGC＝90°，NF∥AC，∴∠NFM＝∠ACG，∴△NMF∽△AGC，∴，∴AG＝＝6，∴AB＝AG＋GB＝6＋2＝8(米)，故电线杆AB的高为8米

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如果两个三角形的两边及其中一边的对角对应相等，那么这两个三角形全等，其逆命题是_______________________，这个逆命题是________命题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知M、N是线段AB的垂直平分线上任意两点，则∠MAN和∠MBN之间关系是____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．

    【特例探究】

    （1）如图1，当tan∠PAB=1，c=4时，a=　　，b=　　；

    如图2，当∠PAB=30°，c=2时，a=　　，b=　　；

    【归纳证明】

    （2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．

    【拓展证明】

    （3）如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3，AB=3，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近似数3.27的准确值a的取值范围是（ ）
    A.3.265≤a＜3.275
    B.3.265＜a＜3.275
    C.3.265≤a≤3.274
    D.3.265＜a≤3.275

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（ ）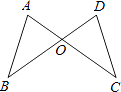
    A.AB=DC
    B.OB=OC
    C.∠C=∠D
    D.∠AOB=∠DOC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠B=40°，AD是BC边上的高，且∠DAC=20°，则∠BAC=________．

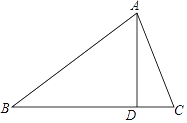
    【答案】70°

    【解析】∵∠B=40°，AD⊥BC，

    ∴∠BAD=90°-40°=50°．

    ∵∠DAC=20°，

    ∴∠BAC=∠BAD+∠DAC=50°+20°=70°．

    【题型】填空题
    【结束】
    16

    【题目】如图所示，E，D是AB，AC上的两点，BD，CE交于点O，且AB=AC，使△ACE≌△ABD，你补充的条件是________

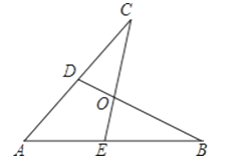
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于，且OD=4，△ABC的面积是（ ）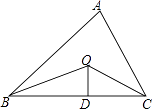
    A.25
    B.84
    C.42
    D.21

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：a3﹣a＝　 　．

    查看答案和解析>>

    同步练习册答案