练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，已知∠A=∠F，AB∥EF，BC=DE，请说明AD∥CF的理由．

    分析 根据平行线的性质得到∠B=∠E，根据全等三角形的性质得到∠ADC=∠FCE，由平行线的判定定理即可得到结论．

    解答 证明：∵BC=DE，
    ∴BD=EC，
    ∵AB∥EF，
    ∴∠B=∠E，
    在△ABD与△FEC中，$\left\{\begin{array}{l}{∠A=∠F}\\{∠B=∠E}\\{BD=CE}\end{array}\right.$，
    ∴△ABD≌△FEC，
    ∴∠ADC=∠FCE，
    ∴AD∥FC．

    点评 此题主要考查了全等三角形的判定与性质，平行线的判定，解决问题的关键是证明△ABD≌△EFC．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．如图，P是等边三角形ABC外一点，PA=3，PB=4，PC=5，求∠BPA的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知AB=AD，BC=DC．求证：AC平分∠BAD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

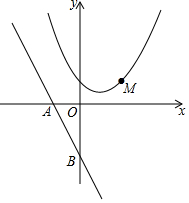    20．直线y=-$\frac{4}{3}$x-4与x轴交于点A，与y轴交于点B，抛物线y=x2-4x+5上的一点M（3，2）．
    （1）求点M到直线AB的距离；
    （2）抛物线上是否存在点P，使得△PAB的面积最小？若存在，求出点P的坐标及△PAB面积的最小值；不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

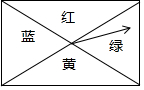    7．如图，一块长宽不等的矩形木板，连接对角线后被分成4个区域，分别涂上红、黄、蓝、绿四色，木板中间装有指针，指针转动停止后，下面两个结论：
    （1）指针指向红、蓝区域的概率与指向黄、绿区域的概率相等；
    （2）指针指向红、黄区域的概率与指向蓝、绿区域的概率相等．
    其中说法正确的是（1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．平面直角坐标系中，A（3，0），B（2，2），P，Q两点在直线x=1上，P在Q的上面，PQ=1，则四边形ABPQ的周长最小值为$\sqrt{5}$+$\sqrt{10}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．关于x的方程$\frac{13m+x}{2}$=4的解是$\frac{2x-3m}{3}$-$\frac{x-1}{4}$=$\frac{1}{6}$x-1的解的5倍，则m=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列各式中一定是二次根式的是（　　）
    A．$\root{3}{16}$B．$\sqrt{a}$C．$\sqrt{-{a}^{2}-1}$D．$\sqrt{{a}^{2}+2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．二次函数y=5（x-1）（x+3）的图象与y轴交点的坐标是（0，-15）．

    查看答案和解析>>

    同步练习册答案