
【题目】某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |

(1)把上表中x,y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式.
(2)当销售单价为多少元时,工艺品厂试销该小工艺品每天获得的利润最大?最大利润是多少?(利润=销售额﹣成本)
【答案】
(1)解:画出图形,如图所示.
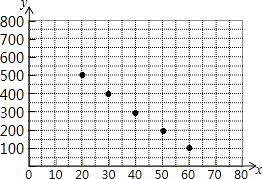
由图可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(20,500),(30,400)两点,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴函数关系式是y=﹣10x+700.
经验证,其他各点也在y=﹣10x+700上
(2)解:设工艺品试销每天获得利润为W元,
由已知得:W=(x﹣10)(﹣10x+700)=﹣10x2+800x﹣7000=﹣10(x﹣40)2+9000,
∵﹣10<0,
∴当x=40时,W取最大值,最大值为9000.
故:当销售单价为40元时,工艺品厂试销该小工艺品每天获得的利润最大,最大利润是9000元
【解析】(1)将表中各点描在坐标系中,根据点的分别可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),根据点的坐标利用待定系数法即可求出该函数关系式式,再验证其余各点是否在该函数关系式的图象上,由此即可得出结论;(2)设工艺品试销每天获得利润为W元,根据“利用=单件利润×销售数量”即可得出W关于x的函数关系式,利用配方法结合二次函数的性质即可解决最值问题.


科目:初中数学 来源: 题型:
【题目】如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,则两圆组成的圆环的面积是( ) 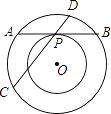
A.16π
B.36π
C.52π
D.81π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 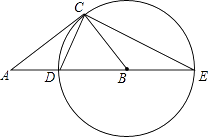
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营一批进价是30元/件的商品,在市场试销中的日销售量y件与销售价x元之间满足一次函数关系.
(1)请借助以下记录确定y与x的函数关系式,并写出自变量x的取值范围;
x | 35 | 40 | 45 | 50 |
y | 57 | 42 | 27 | 12 |
(2)若日销售利润为P元,根据上述关系写出P关于x的函数关系式,并指出当销售单价x为多少元时,才能获得最大的销售利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△DCE、△FEG为等边三角形,边长分别为2、3、5,且从左至右如图排列,连接BF,交DC、DE分别于M、N两点,则△DMN的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x<0)的图象交于A(﹣1,3),B(﹣3,n)两点,直线y=﹣1与y轴交于点C.
(x<0)的图象交于A(﹣1,3),B(﹣3,n)两点,直线y=﹣1与y轴交于点C. 
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com