
证明:(1)在RT△ABH和RT△ADH中,
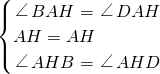
,
∴△ABH≌△ADH(ASA),
∴∠ADH=∠ABH,BH=DH,
∵∠ADB=∠C+∠DBC(三角形的外角性质),∠ABC=∠ABD+∠DBC=5∠ACB,
∴∠C+∠DBC+∠DBC=5∠C,
故有∠DBC=2∠C.
(2)连接HM、HE,
∵M是BC边的中点,DE⊥BC,
∴HM是△BDC的中位线,HE=HD=HB,
∴∠DBC=∠HEB,
由(1)得,∠DBC=∠HEB=2∠C=2∠HME,
又∵∠HEB=∠HME+∠EHM(三角形的外角的性质),
∴∠HME=∠EHM,
∴HE=EM=

BD.
分析:(1)可先证△ABH≌△ADH,这样得出∠ADH=∠ABH,BH=DH,利用三角形的外角可得∠ADB=∠C+∠DBC,再结合∠ABC=∠ABD+∠DBC=5∠ACB,可证得结论.
(2)连接HM、HE,则可得HM是△BDC的中位线,HE=HD=HB,结合(1)∠DBC=2∠C=2∠HME,可得出∠HME=∠EHM,即得出HE=EM,转化后即可得出所要证的结论.
点评:本题考查三角形的中位线定理、线段垂直平分线的性质及直角三角形的斜边中线,属于综合型题目,有一定的难度,解答本题有两点比较关键,①利用中垂线的性质得出△ABH≌△ADH,②掌握直角三角形的斜边中线等于斜边一半得出HE=HD=HB=

BD,另外角的性质在本题中了得到了应用.

 如图,在△ABC中,∠ABC=5∠ACB,BD与∠A的平分线垂直于H,DE⊥BC,若M是BC边的中点,求证:(1)∠DBC=2∠C;(2)EM=
如图,在△ABC中,∠ABC=5∠ACB,BD与∠A的平分线垂直于H,DE⊥BC,若M是BC边的中点,求证:(1)∠DBC=2∠C;(2)EM= BD.
BD. 证明:(1)在RT△ABH和RT△ADH中,
证明:(1)在RT△ABH和RT△ADH中,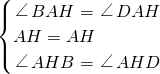 ,
, BD.
BD. BD,另外角的性质在本题中了得到了应用.
BD,另外角的性质在本题中了得到了应用. 

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为