
【题目】在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, ![]() m)(m为非负数),则CA+CB的最小值是_____.
m)(m为非负数),则CA+CB的最小值是_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】写出下列各题中![]() 关于
关于![]() 的函数关系式,并判断
的函数关系式,并判断![]() 是否为
是否为![]() 的一次函数,是否为正比例函数.
的一次函数,是否为正比例函数.
(1)长方形的面积为20,长方形的长![]() 与宽
与宽![]() 之间的函数关系式;
之间的函数关系式;
(2)刚上市时西瓜每千克3.6元,买西瓜的总价![]() 元与所买西瓜
元与所买西瓜![]() 千克之间的函数关系式;
千克之间的函数关系式;
(3)仓库内有粉笔400盒,如果每个星期领出36盒,仓库内余下的粉笔盒数![]() 与星期数
与星期数![]() 之间的函数关系式;
之间的函数关系式;
(4)爸爸为小林存了一份教育储蓄,首次存入10 000元,以后每个月存入500元,存入总数![]() 元与月数
元与月数![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换.旋转变换是几何变换的一种基本模型.经过旋转,往往能使图形的几何性质明白显现.题设和结论中的元素由分散变为集中,相互之间的关系清楚明了,从而将求解问题灵活转化.
问题提出:如图1,![]() 是边长为1的等边三角形,
是边长为1的等边三角形,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() ,求
,求![]() 的最小值.
的最小值.
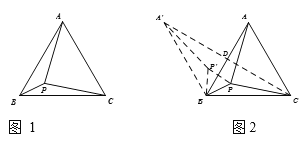
方法通过转化,把由三角形内一点发出的三条线段(星型线)转化为两定点之间的折线(化星为折),再利用“两点之间线段最短”求最小值(化折为直).
问题解决:如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() 、
、![]() ,记
,记![]() 与
与![]() 交于点
交于点![]() ,易知
,易知![]() ,
,![]() .由
.由![]() ,
,![]() ,可知
,可知![]() 为正三角形,有
为正三角形,有![]() .
.
故![]() .因此,当
.因此,当![]() 共线时,
共线时,![]() 有最小值是
有最小值是![]() .
.
学以致用:(1)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() 、
、![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
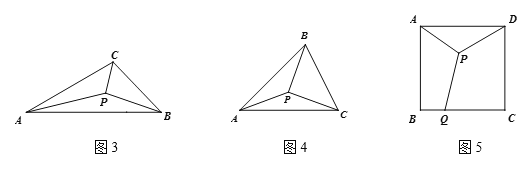
(2)如图4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 内部一点,连接
内部一点,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
(3)如图5,![]() 是边长为2的正方形
是边长为2的正方形![]() 内一点,
内一点,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
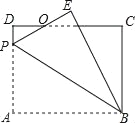
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则DP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作射线
点作射线![]() ,使
,使![]() ,将一直角三角板的直角项点放在点
,将一直角三角板的直角项点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
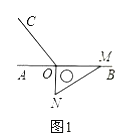
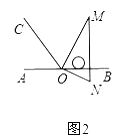
![]() 如图2,将图1中的三角板绕点
如图2,将图1中的三角板绕点![]() 逆时针旋转,使边
逆时针旋转,使边![]() 在
在![]() 的内部,且
的内部,且![]() 恰好平分
恰好平分![]() .此时
.此时![]() __ 度;
__ 度;
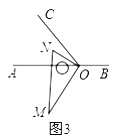
![]() 如图3,继续将图2中的三角板绕点
如图3,继续将图2中的三角板绕点![]() 按逆时针方向旋转,使得
按逆时针方向旋转,使得![]() 在
在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
![]() 将图1中的三角板绕点
将图1中的三角板绕点![]() 按每秒
按每秒![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,若第
的速度沿逆时针方向旋转一周,在旋转的过程中,若第![]() 秒时,
秒时,![]() 三条射线恰好构成相等的角,则
三条射线恰好构成相等的角,则![]() 的值为__ (直接写出结果).
的值为__ (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,射线
,射线![]() .
.
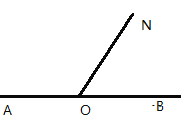
![]() 请画出
请画出![]() 的平分线
的平分线![]() ;
;
![]() 如果
如果![]() ,射线
,射线![]() 分别表示从点
分别表示从点![]() 出发东、西两个方向,那么射线
出发东、西两个方向,那么射线![]() 方向,射线
方向,射线![]() 表示 方向.
表示 方向.
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,在图中找出所有与
时,在图中找出所有与![]() 互补的角,这些角是_ .
互补的角,这些角是_ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌凳,准备修理后支援贫困山区学校,现有甲、乙两木工组,甲每天修桌凳20套,乙每天修桌凳比甲多5套,甲单独修完这些桌凳比乙单独修完多用9天,学校每天付甲组80元修理费,付乙组110元修理费.
(1)问该中学库存多少套桌凳?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:①由甲单独修理;②由乙单独修理;③甲、乙合作同时修理.你认为哪种方案省时又省钱为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com