
分析 (1)先把括号内通分,再把除法运算化为乘法运算,然后把分子分母分解因式后约分即可;
(2)先进行二次根式的乘法运算,然后化简后合并即可.
解答 解:(1)原式=$[{\frac{3x+4}{{({x+1})({x-1})}}-\frac{2}{x-1}}]×\frac{{{{({x-1})}^2}}}{x+2}$
=$[{\frac{3x+4}{{({x+1})({x-1})}}-\frac{{2({x+1})}}{{({x-1})({x+1})}}}]×\frac{{{{({x-1})}^2}}}{x+2}$
=$\frac{3x+4-2x-2}{{({x+1})({x-1})}}×\frac{{{{({x-1})}^2}}}{x+2}$
=$\frac{x+2}{{({x+1})({x-1})}}×\frac{{{{({x-1})}^2}}}{x+2}$
=$\frac{x-1}{x+1}$;
(2)原式=$-3\sqrt{2}+2\sqrt{2}+3\sqrt{2}$
=$2\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了分式的混合运算.


科目:初中数学 来源: 题型:选择题
| A. | 射击运动员射击一次,命中9环 | |
| B. | 今天是星期六,明天就是星期一 | |
| C. | 某种彩票中奖率为10%,买十张有一张中奖 | |
| D. | 在只装有10个红球的布袋中摸出一球,这个球一定是红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
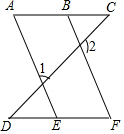 如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说:
如图,1°∠1+∠2=180°,2°∠A=∠F,3°∠C=∠D,任选两个结论作为条件,说明第三个结论正确,也就是说:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com