分析:方法一:首先连接AB、作圆O1的直径AF,连接FB,利用圆周角定理得出∠BAF+∠AFB=90°,进而求出∠C+∠EDB=90° 即可.
方法二:首先连接AD,AO1,CO1,BO1;由于A,B,D,O1四点共圆,根据圆内接四边形的性质知可证得△CDO1≌△ADO1,则AD=CD,DE为等腰△ACD的顶角平分线;由等腰三角形的性质:顶角的平分线与底边上的高重合,进而得出答案.
解答: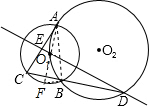
方法一:
证明:如图:
连接AB、作圆O
1的直径AF,连接FB,
∵AF为直径
∴∠BAF+∠AFB=90°
∵∠C=∠F,∠FAB=∠EDB
∴∠C+∠EDB=90°
∴DE⊥AC
方法二:
证明:如图:

连接AD,AO
1,CO
1,BO
1;
∵AO
1=BO
1,
∴弧AO
1=弧BO
1,∠ADO
1=∠BDO
1;
在⊙O
1中,CO
1=BO
1,
∴∠O
1CB=∠O
1BC;
∵A,B,D,O
1四点共圆,
∴∠O
1BC=∠O
1AD=∠O
1CB;
在△CDO
1和△ADO
1中
| | ∠O1DC=∠O1DA | | ∠DCO1=∠DAO1 | | DO1=DO1 |
| |
,
∴△CDO
1≌△ADO
1;
∴AD=CD,∠ADO
1=∠CDO
1;
∴DE⊥AC.
点评:本题主要考查了圆周角定理、圆内接四边形的性质、全等三角形的判定和性质、等腰三角形的性质等知识,综合性较强,难度较大.

 已知:如图,⊙O1与⊙O2相交于A,B两点,圆心O1在⊙O2上,过B点作两圆的割线CD,射线DO1交
已知:如图,⊙O1与⊙O2相交于A,B两点,圆心O1在⊙O2上,过B点作两圆的割线CD,射线DO1交 方法一:
方法一:


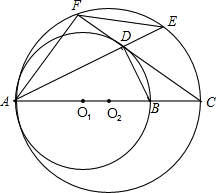 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.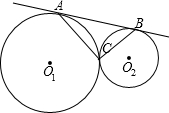 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=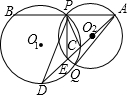 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且